
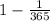 , далее возьмемь третього человека, вероятность того, что его день рождение не совпадеть из первыми двумя равна -
, далее возьмемь третього человека, вероятность того, что его день рождение не совпадеть из первыми двумя равна - 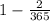 , идем по аналогии и находим вероятности для следующих человек в групе. Общая формула нахождение вероятности будет выглядеть так
, идем по аналогии и находим вероятности для следующих человек в групе. Общая формула нахождение вероятности будет выглядеть так 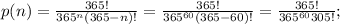
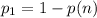 ; Тепер все посчитаем.
; Тепер все посчитаем.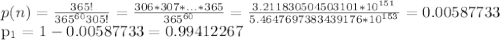
x₁=3; x₂=4; x₃=5
Пошаговое объяснение:
Система уравнений скорее всего будет выглядеть так:
x₁+2x₂+4x₃=31
5x₁+x₂+2x₃=29
3x₁-x₂+x₃=10
Решение методом Крамера.
По правилу треугольников:
| 1 2 4 |
Δ=| 5 1 2 |
| 3 -1 1 |
Δ=1·1·1+2·2·3+4·5·(-1)-3·1·4-(-1)·2·1-1·5·2=1+12-20-12+2-10=-27
| 31 2 4 |
Δ₁=| 29 1 2 |
| 10 -1 1 |
Δ₁=31·1·1+2·2·10+4·29·(-1)-10·1·4-(-1)·2·31-1·29·2=31+40-116-40+62-58=-81
| 1 31 4 |
Δ₂=| 5 29 2 |
| 3 10 1 |
Δ₂=1·29·1+31·2·3+4·5·10-3·29·4-10·2·1-1·5·31=29+186+200-348-20-155=-108
| 1 2 31 |
Δ₃=| 5 1 29 |
| 3 -1 10 |
Δ₃=1·1·10+2·29·3+31·5·(-1)-3·1·31-(-1)·29·1-10·5·2=10+174-155-93+29-100=-135
x₁=Δ₁/Δ=-81/(-27)=3
x₂=Δ₂/Δ=-108/(-27)=4
x₃=Δ₃/Δ=-135/(-27)=5