Question

Маша выписывает по порядку на доску натуральные трехзначные числа. Оказалось, что выписанные Дашей числа (их не меньше трех) образуют конечную геометрическую прогрессию, а первое число равно 128.

а) Могла ли Даша выписать на доске число 686?
Б) Могла ли Даша выписать на доске число 496?
в) Какое наибольшее число могла выписать на доске Даша?

Answer 1

а) да; б) нет; в) 972

Пошаговое объяснение:

а) Пусть геометрическая прогрессия имеет знаменатель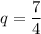 $q=\dfrac{7}{4}$. Тогда получим последовательность $b_1=128,b_2=128\cdot\dfrac{7}{4}=224,b_3=128\cdot\left(\dfrac{7}{4}\right)^2=392,b_4=128\cdot\left(\dfrac{7}{4}\right)^3=686$. Число 686 может быть записано на доске.

б) Заметим, что знаменатель прогрессии q не может быть иррациональным числом: в противном случае второй член прогрессии b₂ = 128q — иррациональное число, что противоречит условию. Значит, q — рациональное число.

Предположим, что 496 является n-ным членом последовательности. Тогда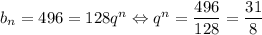 $b_n=496=128q^n\Leftrightarrow q^n=\dfrac{496}{128}=\dfrac{31}{8}$. Поскольку 31 — простое число, оно не является степенью какого-либо другого числа. Значит, n = 1, 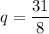$q=\dfrac{31}{8}$. Тогда получаем геометрическую прогрессию $b_1=128,b_2=128\cdot\dfrac{31}{8}=496,b_3=128\cdot\left(\dfrac{31}{8}\right)^2=1922999$ — третий член последовательности не трёхзначный, что противоречит условию. Значит, прогрессии с членом 496 не существует.

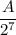в) Пусть A — наибольший возможный член геометрической прогрессии, по условию A < 1000. Тогда $b_n=A=128q^n\Leftrightarrow q^n=\dfrac{A}{128}\Leftrightarrow q^n=\dfrac{A}{2^7}$. Число $\dfrac{A}{2^7}$ является степенью некоторого рационального числа, значит, 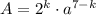$A=2^k\cdot a^{7-k}$, где k — некоторое целое число из промежутка [0, 7], a — положительное нечётное число. Число представимо в таком виде, поскольку на 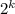$2^k$ можно сократить, в знаменателе останется $2^{7-k}$, далее дробь несократима и является степенью n = 7 - k числа q: $\dfrac{A}{2^7}=\dfrac{2^k\cdot a^{7-k}}{2^7}=\dfrac{a^{7-k}}{2^{7-k}}=\left(\dfrac{a}{2}\right)^{7-k}$. Значит, $2^k\cdot a^{7-k}$.

Переберём все k от 0 до 7:

k = 0: $a^7$. $2^7=128,3^7=2187\Rightarrow a\leq 2\Rightarrow a\leq 1\Rightarrow A\leq 1$k = 1: $2a^6$. $2^6=64, 3^6=729\Rightarrow a\leq 2\Rightarrow a\leq 1\Rightarrow A\leq 2$k = 2: $4a^5$. $3^5=243,4^5=1024\Rightarrow a\leq 3\Rightarrow A\leq 972$k = 3: $8a^4$. $3^4=81,4^4=256\Rightarrow a\leq 3\Rightarrow A\leq 648$k = 4: $16a^3$. $3^3=27, 4^3=64\Rightarrow a\leq 3\Rightarrow A\leq 432$k = 5: $32a^2$. $5^2=25,6^2=36\Rightarrow a\leq 5\Rightarrow A\leq 800$k = 6: $64a$k = 7: $128$ — верно, A = 128.

Наибольшее значение A = 972. Покажем, что оно достигается. Пусть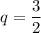 $q=\dfrac{3}{2}$. Тогда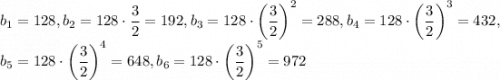 $b_1=128,b_2=128\cdot\dfrac{3}{2}=192,b_3=128\cdot\left(\dfrac{3}{2}\right)^2=288,b_4=128\cdot\left(\dfrac{3}{2}\right)^3=432,\\b_5=128\cdot\left(\dfrac{3}{2}\right)^4=648,b_6=128\cdot\left(\dfrac{3}{2}\right)^5=972$

Таким образом, наибольшее число, которое могла выписать Даша — 972.