К решению прилагается рисунок
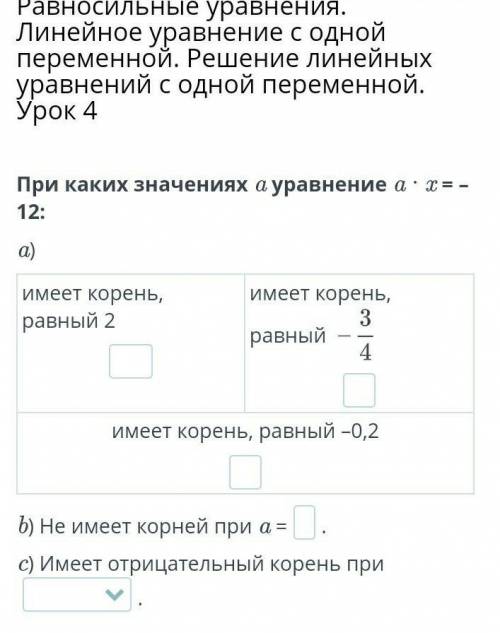
Дано: AF, AE - наклонные
AH - перпендикуляр к плоскости α
EH,FH - проекции
∠AFH = 60°
∠AEH = 30°
HE = 6 см
Найти: FH - ?
Решение: 1) Рассмотрим ΔAEH
ΔAEH - прямоугольный, т.к. AH - перпендикуляр к плоскости α
Т.к. ∠AEH = 30° ⇒ AE = 2AH
Пусть x - AH, тогда 2x - AE
По теореме Пифагора
x² + 6² = (2x)²
x² + 36 = 4x²
4x² - x² = 36
3x² = 36
x² = 12
x = √12
2)Рассмотрим ΔAFH
ΔAEH - прямоугольный, т.к. AH - перпендикуляр к плоскости α
Т.к. ∠AFH = 60° ⇒ ∠FAH = 30° ⇒ FH = 2AF
Пусть y - FH, тогда 2y - AF
По теореме Пифагора
y² + (√12)² = (2y)²
y² + 12 = 4y²
4y² - y² = 12
3y² = 12
y² = 4
y = 2
ответ: FH = 2
1 сторона-20см 2 сторона-18см 3 сторона-14 см
Пошаговое объяснение:
Дано:
(O;r) ∆АВС. M,K, F - точки
Р∆АВС = 52 см. AM : MB = 2 : 3. KC = 6 см.
рішення
нехай одна сторона=x см,тогда AM=2x,MB=3x.
MB=BK=3х(по св-ву отрезков касательной)
AM=AF=2x(по св-ву отрезков касательной)
FC=KC=6 см(по св-ву отрезков касательной)
AB=MB+AM=3x+2x=5x
BC=6+3x
AC=6+2x
Складаємо рівняння
5х + 3х + 6 + 2х + 6 = 52
10х + 12 = 52
10х = 51 - 12
10х = 40
х = 4
одна сторона-4см
АВ = 5 * 4 = 20 см;
ВС = 3 * 4 + 6 = 18 см;
АС = 2* 4 + 6 = 14 см.
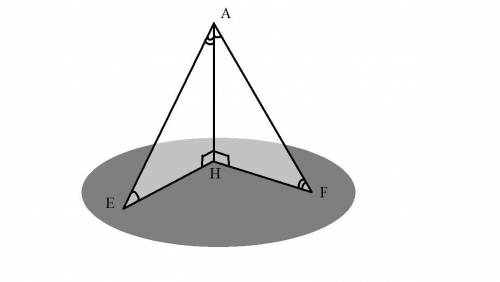
а) При значении а = -6 уравнение имеет корень равный 2.
При значении а = 16 уравнение имеет корень равный -3/4.
При значении а = 60 уравнение имеет корень равный -0,2.
b) При значении а = 0 уравнение не имеет корней.
c) При а > 0 уравнение будет иметь отрицательный корень.
Пошаговое объяснение:
Требуется найти, при каких значениях а уравнение
а)
1. Имеет корень, равный 2.
Подставим вместо х его значение 2 и решим уравнение относительно а:
⇒ При значении а = -6 уравнение имеет корень равный 2.
2. Имеет корень, равный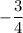 .
.
⇒ При значении а = 16 уравнение имеет корень равный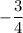 .
.
3. Имеет корень, равный -0,2.
⇒ При значении а = 60 уравнение имеет корень равный -0,2.
b) Не имеет корней.
Уравнение не имеет решения, если при любом значении х, мы не получим верного равенства.Это возможно только тогда, когда а = 0.
Проверим:
⇒ При значении а = 0 уравнение не имеет корней.
с) Имеет отрицательный корень.
Правая часть у нас отрицательная.
При нахождении корня, мы делим правую часть на а. Чтобы корень был отрицательным, то а должно быть положительным.
При делении чисел с разными знаками, частное - отрицательно.⇒ а > 0
⇒ При а > 0 уравнение имеет отрицательный корень.