60) По теореме Пифагора сумма квадратов длин катетов равна квадрату длины гипотенузы, а гипотенуза равна корню из суммы квадратов длин катетов. Заметим, что гипотенуза всегда меньше суммы длин катетов, значит 3 не может быть гипотенузой, т.к 4>3. У нас есть два варианта - а это гипотенуза или 4. Допустим, что гипотенуза- это а. Тогда
А=корень из (3^2+4^2)
А = 5
Теперь второй вариант, 4- это гипотенуза. Тогда 4=корень из (3^2+а^2)
16= 9 + а^2
А^2= 7
А= корень из 7. Значит ответ Г. Надеюсь правильно, в первый раз отвечала
58) во втором В. Там можно решить с уравнения. Пусть х - длина стороны маленького квадрата. Тогда сторона большого - 3х или 24-х. Составляем уравнение. 3х=24-х
х=6. Значит AD= 3*6+8= 26
ответ: В
19/30 или 0.63
Пошаговое объяснение:
1. Вычисляем сумму. (-5+8)+(-0,36+(-0,64))-1 2/3
Получаем : 3+(-0,36+(-0,64))-1 2/3
2. Когда перед выражением в скобках стоит знак "+", тогда оно остается прежним. 3+(-0,36+(-0,64))-1 2/3
Получаем : 3+(-0,36-0,34)-1 2/3
3. Представляем смешанную дробь виде неправильной дроби. 3+(-0,36-0,34)-1 2/3
Получаем : 3+(-0,36-0,34)- 5/3
4.Вычисляем разность 3+(-0,36-0,34)- 5/3
Получаем : 3+(-0,7)- 5/3
5. Раскрываем скобки (не забываем, что когда перед выражением в скобках стоит знак "+", тогда оно остается прежним). 3+(-0,7)- 5/3
Получаем : 3-0,7- 5/3
6. Вычисляем разность 3-0,7- 5/3
Получаем : 19/30 или 0.63
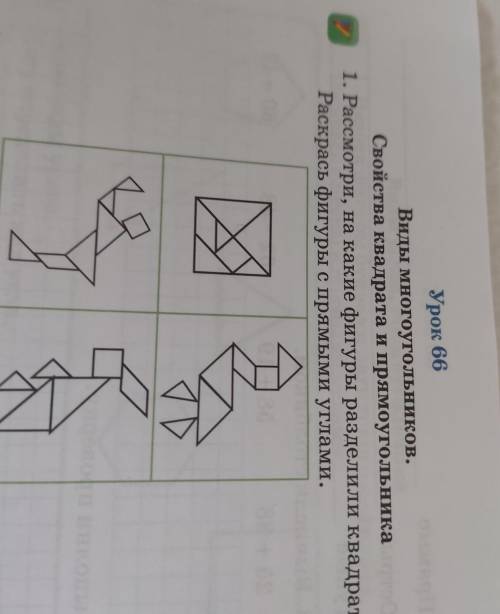
Квадрат разделили на 2 четырехугольника, один из которых квадратом не является, и 5 прямоугольных треугольников.
Определили фигуры с прямыми углами и раскрасили их.
Пошаговое объяснение:
Требуется определить, на какие фигуры разделили квадрат.
Также надо раскрасить фигуры с прямыми углами.
Вспомним определение квадрата и прямоугольного треугольника:
Квадрат — правильный четырёхугольник, у которого все стороны равны и все углы прямые.Прямоугольный треугольник – треугольник, у которого один угол – прямой, т.е. равный 90°.1. На 1 рисунке квадрат разделили на несколько фигур, одна из которых (сиреневая) - квадрат, остальные раскрашенные фигуры - прямоугольные треугольники.
Одна нераскрашенная фигура - четырехугольник, который не является квадратом, так как не имеет прямых углов.
2. На втором рисунке мы найдем также один квадрат и 5 прямоугольных треугольников.
Один нераскрашенный четырехугольник не является квадратом.
3. На 3 рисунке - 1 квадрат и 5 прямоугольных треугольников. И тоже есть четырехугольник, не являющийся квадратом.
4. На 4 рисунке есть 1 квадрат и 4 прямоугольных треугольника.
Нераскрашенная фигура - четырехугольник, который квадратом не является.
Определили фигуры с прямыми углами и раскрасили их.