1); 3); 5); 6).
Пошаговое объяснение:Признаки делимости числа на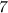 
(для двузначных чисел) :
Число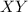 
делится на 
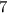, если число 
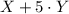делится на .
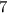Признаки делимости числа на 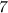(для трёхзначных чисел) :
Число 
делится на 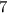, если число 
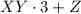делится на .
-----------------------------------------------------------------------------------------------
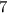1).
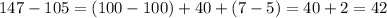
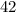- двузначное число ⇒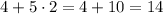 
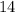делится на 
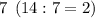, значит 
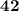делится на 
(
).
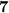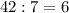2).
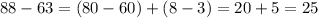
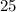- двузначное число ⇒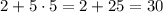 
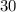нацело не делится на 
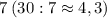, значит 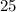не делится на .
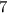3).
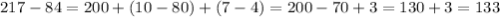
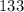- трёхзначное число ⇒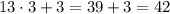 
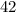делится на 
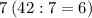, значит 
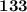делится на (
).
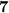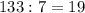4).
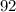- двузначное число ⇒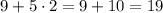 
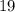нацело не делится на 
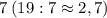, значит 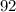не делится на .
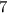5).
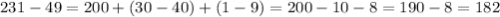
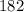- трёхзначное число ⇒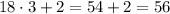 
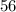делится на 
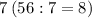, значит 
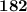делится на 
.
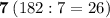6).
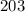- трёхзначное число ⇒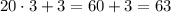 
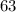делится на 
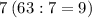, значит 
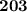делится на (
).
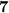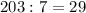x³=x²-7x+7
Перенесем все влево и разложим на множители методом группировки и вынесения общего множителя за скобки:
x^3-x^2+7x-7=0
x^2(x-1)+7(x-1)=0
(x-1)(x^2+7)=0.
Произведение множителей равно 0, если один из множителей равен 0.
Рассматриваем оба варианта:
1) х-1=0
х=1
2) x^2+7=0;
x^2=-7 --в этом уравнении среди действительных чисел нет решения, так как квадрат числа не может быть отрицательным
ответ: х=1
Проверка:
x³=x²-7x+7
1^3=1^2-7×1+7
1=1-7+7
1=-6+7
1=1