Приведем примерный алгоритм получения необходимых данных.
1.Нахождение области определения функции
Определение интервалов, на которых функция существует.
!!! Очень подробно об области определения функций и примеры нахождения области определения тут.
2.Нули функции
Для вычисления нулей функции, необходимо приравнять заданную функцию к нулю и решить полученное уравнение. На графике это точки пересечения с осью ОХ.
3.Четность, нечетность функции
Функция четная, если y(-x) = y(x). Функция нечетная, если y(-x) = -y(x). Если функция четная – график функции симметричен относительно оси ординат (OY). Если функция нечетная – график функции симметричен относительно начала координат.
4.Промежутки знакопостоянства
Расстановка знаков на каждом из интервалов области определения. Функция положительна на интервале - график расположен выше оси абсцисс. Функция отрицательна - график ниже оси абсцисс.
5. Промежутки возрастания и убывания функции.
Для определения вычисляем первую производную, приравниваем ее к нулю. Полученные нули и точки области определения выносим на числовую прямую. Для каждого интервала определяем знак производной. Производная положительна - график функции возрастает, отрицательна - убывает.
6. Выпуклость, вогнутость.
Вычисляем вторую производную. Находим значения, в которых вторая производная равна нулю или не существует. Вторая производная положительна - график функции выпукл вверх. Отрицательна - график функции выпукл вниз.
7. Наклонные асимптоты.
Пример исследования функции и построения графика №1
Исследовать функцию средствами дифференциального исчисления и построить ее график.
Объем фигуры 176 см³.
Пошаговое объяснение:
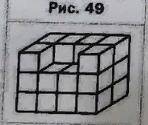
Найти объем изображенной на рисунке фигуры, составленной из кубиков с ребром 2 см.
1) На рисунке видим прямоугольный параллелепипед с выемкой из которой вынули 2 маленьких кубика.
Тогда объем фигуры (Vф) равен разности объемов большого параллелепипеда (Vб) и выемки - малого параллелепипеда (Vм).
Vф = Vб - Vм.
Объем прямоугольного параллелепипеда равен произведению трех его измерений: длины (a), ширины (b), высоты (c):V = abc.
2) Найдем длину, ширину, высоту большого параллелепипеда, не обращая пока внимания на выемку (то есть считаем его целым параллелепипедом).
Ребро маленького кубика равно 2 см.
По длине таких кубиков поместилось 4.
Тогда длина большого параллелепипеда:
4 · 2 см = 8 см.
По ширине кубиков содержится 2.
Ширина большого параллелепипеда:
2 · 2 см = 4 см.
По высоте размещено 3 кубика.
Высота большого параллелепипеда:
3 · 2 см = 6 см.
3) Найдем объем большого параллелепипеда:
Vб = 8 см · 4 см · 6 см = 192 см³.
4) Определим размеры малого параллелепипеда.
Из большого параллелепипеда вынули малый параллелепипед, состоящий из двух маленьких кубиков.
Его длина: 2 · 2 см = 4 см;
ширина 1 · 2 см = 2 см;
высота 1 · 2 см = 2 см.
5) Найдем объем вынутого малого параллелепипеда.
Vм = 4 см · 2 см · 2 см = 16 см³.
6) Найдем объем фигуры.
Vф = Vб - Vм = 192 см³ - 16 см³ = 176 см³
Объем фигуры 176 см³.