1) Продолжение фразы: Математическая дробь может быть использована как часть пропорции. (а/в=1/3)
Математическая дробь может быть использована как замена процентов. (25% = 25/100 = 1/4)
2) Предложения из 5 слов про дроби:
Дробь – часть (или несколько) целого (1:5*2=2/5)
Дроби нужны для перевода величин. (1 Гкал = 4,2 ГДж)
Курс обмена валют – десятичная дробь. (Курс доллара – 73,63 рубля)
Дробью измеряются площади сельскохозяйственных угодий (сотка это и 100кв.м и 1/100 часть гектара.)
Дроби применяются для вычисления времени (3/4 часа =45мин, квартал =1/4 года)
Дроби нужны для деления целого (в быту – суп на порции)
Дроби нужны для нахождения числа. (число, 2/3 которого равны 1000, это 1500)
Одни величины выражаются дробями других (1мм = 1/100м)
Результаты очков конкурсантов – часто дробные. (9, )
Процент магазинной скидки – это дробь. ( 20% скидки от 300 рублей –это уменьшение на 1/5, на 60 рублей)
Рукав три четверти – это дробь ( мода)
Пол-царства в сказках – это дробь! (литература)
Четвертушка блокадного хлеба – это дробь. (жизнь)
3) Науки где применяются дроби:
Агрономия, Антропология, Астрономия, Археология, , Биология, Геология, География, История, Кораблестроение, Космонавтика, Математика, Материаловедение, Машиностроение, Медицина, Механика ,Нанотехнология, Педагогика, Пищевые технологии и Кулинария, Политология , Радиотехника, Социология, Строительство и Архитектура, Теплотехника, Физика, Химия, Экономика
Трудно найти, где НЕ применяется дроби!
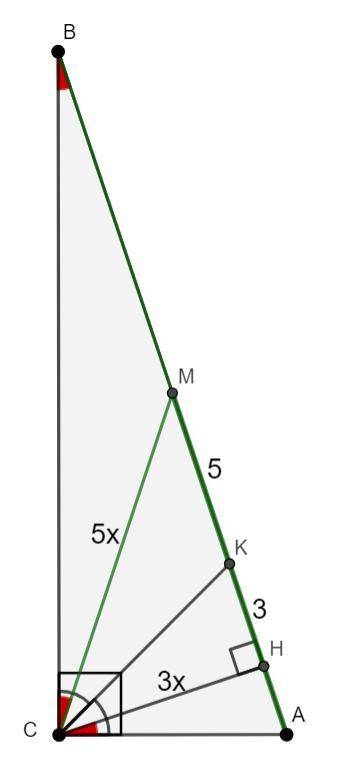
Поэтому K лежит на отрезке MH.
1.
Рассмотри ∠ACH и ∠ABC:
CA⊥BA и CH⊥BH по условию;
∠ACH = ∠ABC, как углы с взаимно перпендикулярными сторонами.
Медиана прямоугольного треугольника, проведённая к гипотенузе, равна половине гипотенузы.Поэтому CM = BM, тогда ΔBMC - равнобедренный.
Углы при основании равнобедренного треугольника равны.Поэтому ∠MBC = ∠MCB, откуда ∠ACH = ∠MCB (т.к. ∠ACH = ∠MBC).
∠ACK = ∠BCK, как углы при биссектрисе;
∠ACH = ∠MCB;
Тогда ∠ACK - ∠ACH = ∠BCK - ∠MCB;
∠HCK = ∠MCK.
Биссектриса треугольника делит сторону треугольника на отрезки, пропорциональные прилежащим сторонам.2.
Рассмотрим ΔMCH:
CK - биссектриса MCH, поскольку ∠HCK = ∠MCK;
Тогда справедливо равенство  ;
;
Пусть CM = 5x, тогда CH = 3x;
HM = HK+KM = 3+5 = 8;
ΔMCH - прямоугольный (CH⊥MH ⇒ ∠CHM = 90°);
Тогда по теореме Пифагора получим:
CH²+HM² = CM²;
(3x)²+8² = (5x)²;
9x²+64 = 25x²;
64 = 16x²;
x² = 64:16 = 2²;
x = 2.
CM = 5x = 5·2 = 10;
CH = 3x = 3·2 = 6.
3.
CM = BM = MA;
MA = 10;
AB = 2·MA = 2·10 = 20;
AH = MA-HM = 10-8 = 2.
4.
Рассмотрим ΔCHA:
∠CHA = 90°; AH = 2; CH = 6;
По теореме Пифагора найдём AC:
AC² = CH²+AH² = 6²+2² = 36+4 = 2²·10;
AC = 2√10.
5.
Рассмотрим ΔABC:
∠ACB = 90°; AC = 10√2; AB = 20;
По теореме Пифагора надём BC:
BC² = AB²-AC² = 20²-40 = 400-40 = 6²·10;
BC = 6√10.
6.
Рассмотрим ΔCHK:
∠CHK = 90°; CH = 6; HK = 3;
По теореме Пифагора найдём CK:
CK² = CH²+HK² = 6²+3² = 36+9 = 3²·5;
CK = 3√5.
ответ: AB = 20; BC = 6√10; AC = 2√10; CK = 3√5.
е=12345-5432
е=6913
12345-6613=5432
5432=5432
5643:к=99
к=5643:99
к=57
5643:57=99
99=99
568*у=428272
у=428272:568
у=754
568*754=428272
428272=428272
Х+1047=8591
х=8591-1047
х=7544
7544+1047=8591
8591=8591
Ну мы решаем так.А в каком ты классе?