Любой объект (изделие, машина или система) обладает характерными свойствами. Некоторые из этих свойств полезны, но другие бывают более или менее нежелательными. Наиболее важное свойство из всех - ϶ᴛᴏ основная функция изделия, потому что она потребителю в удовлетворении его нужд. Другими желательными свойствами бывают приятный внешний вид, легкость перемещения, безопасность, долговечность и надежность. Прежде чем приступить к конструированию, конструктор должен , должна быть в сотрудничестве с потребителем, составить перечень желаемых свойств изделия. В процессе конструирования, когда изделие создается, именно эти свойства определяют выбор принимаемых конструктивных решений.
К сожалению, нельзя конструировать изделия таким путем, чтобы желаемые свойства определялись одно за другим, так как эти свойства являются независимыми переменными. При этом принято считать, что среди всех можно выделить пять базовых свойств, которые в сумме полностью определяют изделие. В целом таким свойством для изделия является структура (ᴛ.ᴇ. элементы изделия и их взаимосвязь), а для каждого элемента – форма, материал, размеры, поверхность. Важно подчеркнуть, что эти свойства являются переменными, которыми конструктор может манипулировать, а изделие создается последовательными решениями вопросов, связанных с этими переменными. Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, все другие свойства, как полезные, так и нежелательные, выводятся из этих базовых свойств. При этом, поскольку эта цель не всегда достигается, крайне важно различать желаемые свойства и фактически полученные свойства, приходя, таким образом к следующей модели процесса конструирования
Для начала поработаем со вторым выражением. Первые три слагаемых свернем в квадрат разности: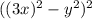 
; В следующих двух слагаемых вынесем общий множитель "40": 
; В итоге получим следующее уравнение: 
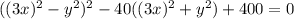. В скобках мы видим похожие выражения, отличающиеся лишь знаком посередине (такие выражение называются сопряженными). А хотелось бы видеть там равные (строго говоря тождественные) выражения. Пусть в первой скобке вместо 
будет стоять 
; Это приведет к тому, что придется убавить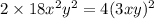 
; В итоге: 
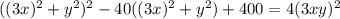; Слева стоит квадрат суммы. Уравнение примет вид: 
; Сворачивая еще раз: 
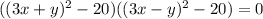; Получаем серию прямых: 
; А теперь приступим к рассмотрению первого уравнения.
Это уравнение задает круг с центром в точке (0, 0) и радиусом 
; Рассмотрим прямую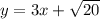 
; Найдем радиус окружности с центром в начале координат, которая касается данной прямой. Это легко сделать из подобия треугольников. 
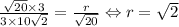; Значит, круг касается всех этих четырех прямых. Достаточно найти только координаты касания с любой из прямых. Это делается так же, как и находился радиус окружности. Для той же прямой это координаты 
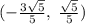; Ну а все решения:
Пошаговое объяснение:
ТЕОРЕМА:
СУММА СМЕЖНЫХ УГЛОВ РАВНА 180°
(1)
ОТВЕТ: 68°
(2)
ОТВЕТ: 108°