 , лежит на перпендикуляре, проведённым из точки А к этой прямой.
, лежит на перпендикуляре, проведённым из точки А к этой прямой. можно провести в плоскости, перпендикулярной прямой
можно провести в плоскости, перпендикулярной прямой  .
. будет нормальным вектором плоскости и точка А лежит в этой плоскости.
будет нормальным вектором плоскости и точка А лежит в этой плоскости.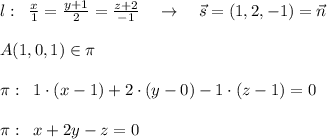
 и плоскости
и плоскости 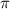 .
. 
 является серединой отрезка
является серединой отрезка 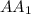 .
.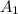 .
.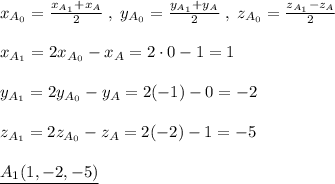
Пусть первое число- x
Второе-y
Произведение будет равно 100
А сумма 101 :
x+y=101 x=101-y
x×y=100 x×y=100
(101-y)×y=100
-y^2+101y=100 /×(-1)
y^2-101y+100=0
D= b^2-4ac
D= -101^2-4×1×100= 10.201-400= 9801>0, 2 корня
y1=b+√D/2a=(101+√9801)/2×1=(101+99)/2=100
y2=b-√D/2a=(101-√9801)/2×1=(101-99)/2=1
x=100
y=1
Проверка:
x+y=101
100+1=101
x×y=100
100×1=100
ответ: 100 ; 1