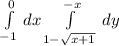
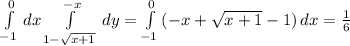
Пошаговое объяснение:
1) 5*109 = 545 - фиолетовый квадратик справа
5*110 = 550 - фиолетовый квадратик внизу
550 - 5 = 545; 5 - синий квадратик
2) 9*109 = 981 - фиолетовый квадратик справа
110 - синий квадратик слева
9*110 = 990 - фиолетовый квадратик внизу
990 - 9 = 981; 9 - синий квадратик справа
3) 4*201 = 804 - фиолетовый квадратик справа
4*200 = 800 - фиолетовый квадратик внизу
800 + 4 = 804; 4 - желтый квадратик
4) 3*301 = 903 - фиолетовый квадратик справа
300 - желтый квадратик слева
3*300 = 900 - фиолетовый квадратик внизу
900 + 3 = 903; 3 - желтый квадратик справа
Исходя из неравенства, мы знаем, что угол находится в третьей четверти. Значит, косинус этого угла также будет отрицателен. Из основного тригонометрического тождества находим этот косинус.
Теперь извлекаем корень, но не забываем добавить перед ним знак минус.
Теперь можем найти и тангенс.
Зная тангенс, находим котангенс.
ответ: .
.