Пошаговое объяснение:
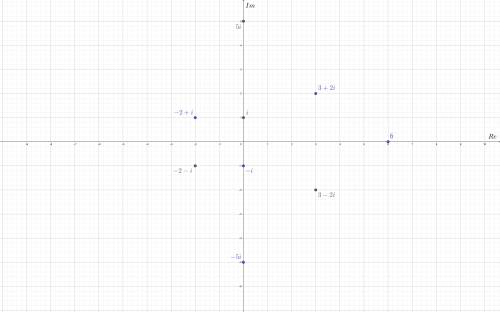
Точка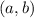 
на комплексной плоскости изображает число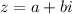 
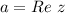- действительная часть числа (Real)
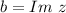- мнимая часть числа (Imaginary)
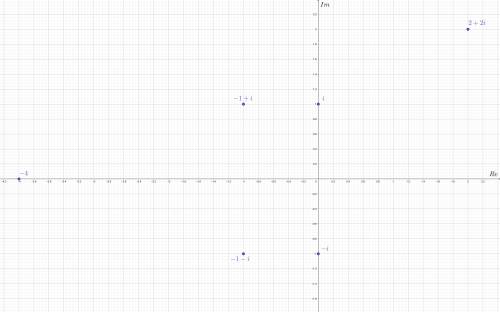
В соответствии с этим строим точки для 16.1. (Картинка 1)
Комплексно-сопряженные числа — пара комплексных чисел, обладающих одинаковыми действительными частями и равными по абсолютной величине противоположными по знаку мнимыми частями.
Т.е. сопряженным для числа 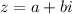будет являться число 
.
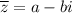В графическом представлении это означает, что сопряженное число будет являться отражением исходного числа относительно действительной оси (оси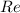 
).
На Картинке 2 серым обозначены исходные точки и синим - комплексно-сопряженные с ними.
d²y/dx²=2*dy/dx
Можно переписать:
y"=2y' - это линейное однородное ДУ второго порядка с постоянными коэффициентами.
y"-2y'=0 (1)
Составим и решим характеристическое уравнение:
р²-2p=0
p*(p-2)=0
p₁=0
p₂=2
Получены два различных действительных корня, поэтому общее решение имеет вид:
y=C₁*e^(p₁*x)+C₂*e^(p₂*x), где p₁ и p₂ - корни характеристического уравнения, C₁ и C₂ - константы.
y=C₁*e^(0*x)+C₂*e^(2*x)
y=C₁+C₂*e^(2*x) - общее решение (2).
Теперь нужно найти частное решение, соответствующее заданным начальным условиям. Наша задача состоит в том, чтобы найти такие значения констант С₁ и С₂, чтобы выполнялись оба условия.
Сначала используем начальное условие y(0)=3/2:
y(0)=C₁+C₂*e^(2*0)=C₁+C₂
Согласно начальному условию получаем первое уравнение:
C₁+C₂=3/2 (3)
Далее берем общее решение (2) и находим производную:
y'=(C₁+C₂*e^(2*x))'=0+2*C₂*e^(2*x)=2*C₂*e^(2*x)
Используем второе начальное условие y'(0)=1:
y'(0)=2*C₂*e^(2*0)=2*C₂
2*C₂=1
C₂=1/2 (4)
Теперь поддставим (4) в (3):
C₁+1/2=3/2
C₁=1 (5)
Остается подставить (4) и (5) в (2):
y=1+3/2*e^(2*x) - частное решение.
ответ: y=C₁+C₂*e^(2*x) - общее решение
y=1+3/2*e^(2*x) - частное решение
Подробнее - на -
Пошаговое объяснение:
три
Пошаговое объяснение:
7: 2 =6 (остаток 1)