
1) -3
2) 0
3) ∞
Пошаговое объяснение:
Для вычисления предела на бесконечности частного двух многочленов можно сравнить степени многочленов - если степень числителя больше, то предел частного будет равен бесконечности. если степени одинаковые, то предел будет равен отношению коэффициентов при старших степенях. Если степень в значменателе больше, то предел будет равен нулю. Примеры на все три случая:
1) 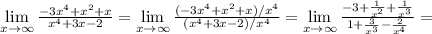
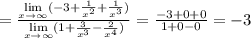
2) 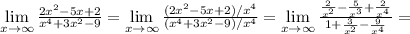
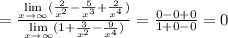
3)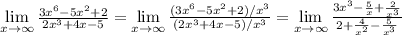
В числителе стоит бесконечно большая функция, знаменатель стремится к 2 (то есть имеет конечный предел), значит частное будет бесконечно большим.
a)x=1
b)x=1
в)x₁=0,x₂=5
Пошаговое объяснение:
Прости дальше не знаю скачай приложение photomatch советую оно для математики...