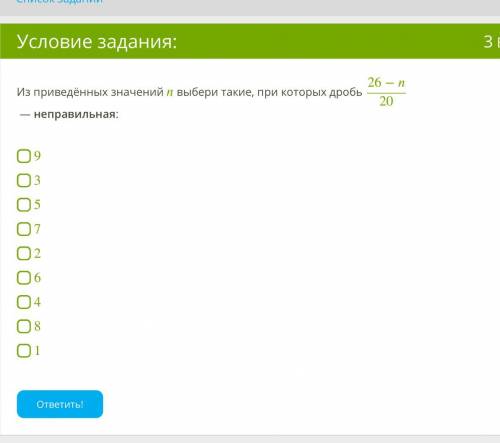
Итак, в задаче необходимо узнать среднюю скорость, которую можно найти как отношение всего пройденного пути ко времени, затраченному на весь путь.
Средняя скорость – эта скорость, которую должно иметь тело (в данном случае автомашина), чтобы пройти то же расстояние за то же время, только двигаясь всегда равномерно (т.е. скорость не должна меняться по величине).
Очевидно, что в общем случае машина не двигается равномерно, так как есть моменты ускорения машины (например, в начале движения из состояния покоя) и моменты замедления (перед остановкой), хотя в этой задаче оно было действительно равномерным (но разным по величине при движении туда и обратно).
Обозначим расстояние между городами – S, время движения в прямом пути – t1, время движения в обратном пути – t2. Тогда:
υср=S+St1+t2(1)
Найдем время t1 и t2:
t1=Sυ1(2)
t2=Sυ2=2Sυ1(3)
Подставим полученные выражения (2) и (3) в (1):
υср=S+SSυ1+2Sυ1
υср=S+SSυ1+2Sυ1=2S⋅υ13S=23υ1
Не будем переводить числовые исходные данные в систему СИ, поскольку ответ нужно получить в км/ч. Численный ответ равен:
υср=2360=40км/ч
ответ: 40 км/ч.
Источник: https://easyfizika.ru/zadachi/kinematika/rasstoyanie-mezhdu-dvumya-gorodami-avtomashina-proehala-so-skorostyu-60-km-ch
Пошаговое объяснение:
Дано:
ΔABC
BE - биссектриса, AD - медиана
BE ⊥ AD
BE = AD = 16
Найти:
стороны ΔABC
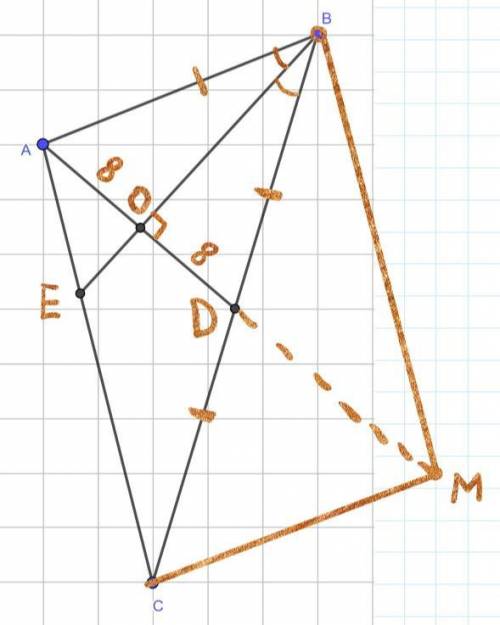
Пусть O - точка пересечения AD и BE, тогда BO - высота и биссектриса ΔABD ⇒ ΔABD - равнобедренный (AB = BD) и BO - медиана ⇒ AO = OD = 8, BC = 2AB
Заметим, что в ΔABC: EC ÷ AE = BC ÷ AB = 2 ( свойство биссектрисы BE) ⇒ EC = 2AE ⇒ AC = AE + EC = 3AE
Проведем через точку C прямую, параллельную AB, а через точку B прямую, параллельную AC, то есть достроим ΔABC до параллелограмма ABMC, где M - точка пересечения проведенных прямых, тогда точка D - пересечение диагоналей построенного параллелограмма.
Рассмотрим ΔAOE и ΔBOM, они подобны по 2-м углам ⇒ BO ÷ OE = BM ÷ AE. Учитывая, что BM = AC получаем BO ÷ OE = 3.
Пусть OE = x, тогда BO = 3x; x + 3x = 16; 4x = 16; x = 4 ⇒ OE = 4; BO = 12
по теореме Пифагора из ΔABO: AB² = 8² + 12² = 208 ⇒ AB = 4√13; BC = 8√13
по теореме Пифагора из ΔAOE: AE² = 8² + 4² = 80 ⇒ AE = 4√5 ⇒ AC = 12√5
это числа 5,4,3,2,1