Делим все члены многочлена на 3/4 х^2 + 2*4/3x - 4/3 =0 x^2 + 8/3x - 4/3 =0 Надо найти такие числа, у которых произведение равно -4/3, а сумма -8/3. Сложно найти эти числа, воспользуясь теоремой Виета .
Этноним скифы и его упоминаниеСкифы, как и другие близкородственные им народы, обитавшие в I тыс. до н.э. в евразийских степях, не имели своей письменности, и потому их социальную и политическую историю приходится воссоздавать преимущественно на основе сведений, сохраненных в инокультурных источниках, и по археологическим данным.Имя скифов, известное нам прежде всего из сочинений греческих и латинских авторов, использовалось там в разных значениях. Зачастую древние писатели именовали скифами широкий круг народов, обитавших в ту эпоху на обширных пространствах евразийского степного пояса и обладавших во многом сходной культурой. Но тщательное изучение употребления этого имени в древних источниках свидетельствует, что сами себя именовали так лишь обитатели Северного Причерноморья и Приазовья или даже первоначально только одно племя, в первые века I тыс. до н.э. подчинившее себе прочее население этого региона и создавшее на этой основе мощный союз племен, позже переросший в раннегосударственное образование. Греческие поселенцы, начавшие с VII в. до н.э. активную колонизацию северного побережья Черного моря, первоначально вошли в соприкосновение именно с этим народом. Со временем, все более расширяя круг своих знаний об обитателях евразийских степей и обнаруживая в их культуре и образе жизни много сходного с тем, что уже было известно им о скифах, греки стали обозначать все народы этого круга именем того из них, который был знаком им раньше и лучше других. Так термин «скифы» приобрел расширительное значение. Но многие античные авторы сохранили понимание и его конкретного этно-исторического смысла и отличали собственно скифов от других степных народов, имена которых также были им известны, — от савроматов, массагетов, исседонов и т. д.Изображение хищника. Курган Кулановского. Крым.Язык
(Метод Лагранжа).
Произвольную постоянную примем за функцию от .
.
Подставим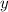 и
и 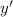 в исходное уравнение:
в исходное уравнение:
Отдельно найдем полученный неопределенный интеграл:
Отсюда получаем что:
Отсюда получаем что:
Теперь подставим в формулу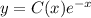 :
:
В итоге окончательно получаем:
(Метод Бернулли)
Пусть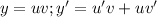 тогда:
тогда:
Подставим найденное значение в
в 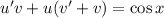 :
:
В предыдущем данный интеграл был найден методом интегрирования по частям, поэтому не будет здесь его искать а просто подставим уже найденный.