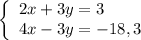
Так как во 2 уравнении перед "х" стоит коэффициент 4, а ему противоположным числом является число (-4) , то число, на которое можно домножить 1 уравнение системы, чтобы получить в уравнениях противоположные коэффициенты перед "х" , это число (-2) . Получим
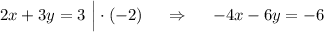
Тогда система будет такой: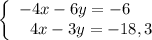 
.
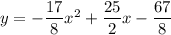
Пошаговое объяснение:
Уравнение параболы в общем виде записывается следующим образом:
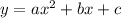
где 
, 
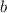и 
-- коэффициенты, которые нам необходимо найти.
Подставим известные нам точки в уравнение параболы и составим систему из трёх уравнений:
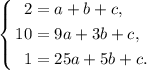
Эту систему можно решать по-разному, дело вкуса. Даю простейшее решение с выражением каждого неизвестного по-очереди.
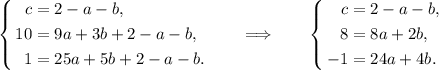
Умножим второе уравнение на 2 и вычтем из третьего второе, чтобы избавиться от :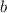
Отсюда видно, что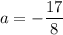 
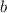, получаем из второго уравнения, а из первого:
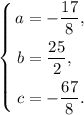
Таким образом, 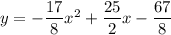- уравнение нашей параболы.
любое целое число a можно представить в виде 3p+r,
где r может принимать лишь значения 0, 1 или 2.
p это какое-то целое число. По сути это деление на 3 с остатком.
Итак, a = 3p+r,
Подставим это значение в исходное выражение:
52a + 112 = 52·(3p+r) + 112 = 3·52·p + 52r + 112.
Эта сумма делится нацело на 3 тогда и только тогда, когда на 3 нацело делится (52r + 112) = R.
Переберём все допустимые значения r.
r = 0, тогда R = 112, на 3 не делится
r = 1, тогда R = 52 + 112 = 164, на 3 не делится.
r = 2, тогда R = 52·2 + 112 = 104 + 112 = 216, делится нацело на 3. Подходит.
ответ. При a = 3p + 2, где p - целое.
ответ: на -2
Пошаговое объяснение:
2x+3y = 3;
4x-3y= -18, 3
надо умножить на минус два.
-2*2x+(-2)*3y = -2*3;
4x-3y = -18, 3
получим
-4x-6y = -6
4x-3y = -18, 3