
Пошаговое объяснение:
1
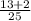
2
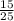
3 Скоротити на 5

Sполн=1032 см²
V=1512 см3
Пошаговое объяснение:
V=Sосн*H
S oсн=√ (p * (p-a) * (p-b) * (p-c))
p=P/2. P=a+b+c
p = (10+17+21) / 2
p=24
S=√ (24 * (24-10) * (24-17) * (24-21))
S=84
V=84*18
Площадь боковой поверхности треугольной призмы будет:
Sбок=18*(10+17+21)=864 см²
Для нахождения площади основания можно воспользоваться формулой Герона для нахождения площади треугольника, когда известны только длины его сторон, но неизвестна высота:
S=√p(p-a)(p-b)(p-c) (под корнем всё выражение!), где a,b,c- стороны треугольника, p- полупериметр треугольника, p=(a+b+c)/2.
p=(10+17+21)/2=24
S=√24(24-10)(24-17)(24-21)=√24*14*7*3=√7056=84 см²
Полная поверхность призмы равна:
Sполн=Sбок+2Sосн
Sполн=864+2*84=864+168=1032 см²
Sполн=1032 см²
3/5
Пошаговое объяснение:
13/25+ 2/25= 15/25=3/5