Пошаговое объяснение:
Систе́ма счисле́ния (англ. numeral system или system of numeration) — символический метод записи чисел, представление чисел с письменных знаков. Система счисления: даёт представления множества чисел (целых и/или вещественных); даёт каждому числу уникальное представление...
Системы Счисления бывают позиционные и непозиционные . На картинке выше символьная и римская СС являются хорошим примером непозиционной системы счисления. Как не переставляйте кружочки, смысл не поменяется их все равно будет десять.
В позиционной СС от позиции(разряда) цифры зависит ее значение. Например число 685 = 600(сотни) + 80(десятки) + 5(единицы), можно записать иначе 685 = 6 * 100 + 8 * 10 + 5 * 1. Если бы число 685 было непозиционным, то мы бы записали так, 685 = 6+8+5 = 19.
Для перевода числа из десятичной системы счисления в любую другую, необходимо это число разделить уголком на основание системы счисления. А в ответ записать остатки от деления в обратном порядке.
3628 если это число записано в десятичной системе то оно будет выглядеть так же.
в восьмеричной системе - будет выгладить( 3628 делим столбиком на 8 получаем 453 и 4 в остатке ) 4544
в шестнацатиричной - ( 3628 : 16 = 226 и 12 в остатке ) - 226С
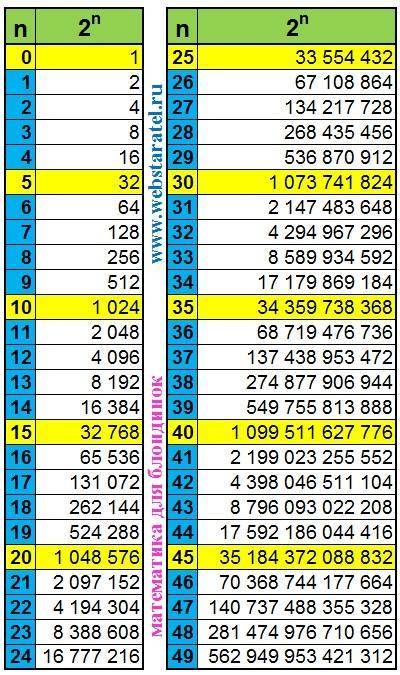
в двоичной (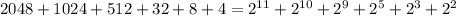 
) = 1 1 1 0 0 0 1 0 1 1 0 0
а ты решай к какой СС отнести число 3628
задачи по теории вероятностей, мы постоянно используем одну и ту же формулу, которая одновременно является классическим определением вероятности:Классическое определение вероятности: p = k/n где k — число благоприятных исходов, n — общее число исходов (см. «Тест по теории вероятностей»).И эта формула прекрасно работает до тех пор, пока задачи были легкими, а числа, стоящие в числителе и знаменателе — очевидными.Однако последние пробные экзамены показали, что в настоящем ЕГЭ по математике могут встречаться значительно более сложные конструкции. Отыскание значений n и k становится проблематичным. В таком случае на приходит комбинаторика. Ее законы работают там, где искомые значения не выводятся непосредственно из текста задачи.В сегодняшнем уроке не будет строгих формулировок и длинных теорем — они слишком сложны и, к тому же, совершенно бесполезны для решения настоящих задач B6. Вместо этого мы рассмотрим простые правила и разберем конкретные задачи, которые действительно встречаются на ЕГЭ. Итак, поехали!Число сочетаний и факториалыПусть имеется n объектов (карандашей, конфет, бутылок водки — чего угодно), из которых требуется выбрать ровно k различных объектов. Тогда количество вариантов такого выбора называется числом сочетаний из n элементов по k. Это число обозначается Cnk и считается по специальной формуле.Обозначение:Число сочетаний из n элементов по kВыражение n! читается как «эн-факториал» и обозначает произведение всех натуральных чисел от 1 до n включительно: n! = 1 · 2 · 3 · ... · n.Кроме того, в математике по определению считают, что 0! = 1 — подобный бред редко, но все же встречается в задачах по теории вероятностей.Что дает нам эта формула? На самом деле, без нее не решается практически ни одна серьезная задача.К сожалению, в школе совершенно не умеют работать с факториалами. Кроме того, в формуле числа сочетаний очень легко запутаться: где стоит и что обозначает число n, а где — k. Поэтому для начала просто запомните: меньшее число всегда стоит сверху — точно так же, как и в формуле определения вероятности (вероятность никогда не бывает больше единицы).Для лучшего понимания разберем несколько простейших комбинаторных задач:Задача. У бармена есть 6 сортов зеленого чая. Для проведения чайной церемонии требуется подать зеленый чай ровно 3 различных сортов. Сколькими бармен может выполнить заказ?Тут все просто: есть n = 6 сортов, из которых надо выбрать k = 3 сорта. Число сочетаний можно найти по формуле:Число сочетаний из 6 элементов по 3 Задача. В группе из 20 студентов надо выбрать 2 представителей для выступления на конференции. Сколькими можно это сделать?Опять же, всего у нас есть n = 20 студентов, а выбрать надо k = 2 студента. Находим число сочетаний:Число сочетаний из 20 элементов по 2
