УМОЛЯЮ ВАС нужно привести дроби к наименьшему общему знаменателю 1. 1/2 и 1/3
2. 2/5 и 3/8
3. 2/6 и 1/3
4. 7/10 и 1/30
5. 1/12 и 1/18
6. 3/20 и 7/30
7. 4/25 и 11/30
8. 1/2 и 1/3
9. 11/24 и 5/12
10. 3/18 и 5/16
11. 4/28 и 4/35
12. 3/17 и 2/11
13. 1/200 и 1/30
14. 5/2 и 7/3
15. 11/22 и 1/2
16. 12/24 и 3/6

👇

Увидеть ответ

Ответ:

iLFid

07.05.2023

1. 3/6 и 2/6

2. 16/40 и 15/40

3. 1/3 и 1/3

4. 21/30 и 1/30

5. 3/36 и 2/36

6. 9/60 и 14/60

7. 24/150 и 55/150

8. как 1

9. 11/24 и 10/24

10. 8/48 и 15/48

11. 5/35 и 4/35

12. 33/187 и 34/187

13. 3/600 и 20/600

14. 15/6 и 14/6

15. 1/2 и 1/2

16. 1/2 и 1/2

4,6(48 оценок)

Открыть все ответы

Ответ:

arisha20003000

07.05.2023

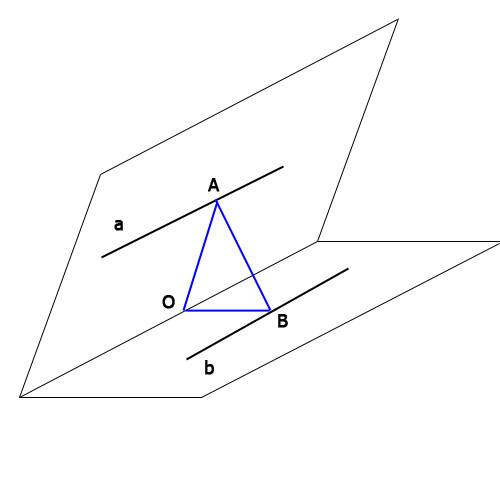
1) Получаем треугольник AOB (см.рис1), стороны которого нам известны (AO=10 см, BO = 6 см, AB = 14 см). Из этого треугольника по теореме косинусов:

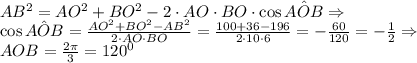$\\AB^2=AO^2+BO^2-2\cdot AO\cdot BO\cdot\cos\hat{AOB}\Rightarrow\\\cos\hat{AOB}=\frac{AO^2+BO^2-AB^2}{2\cdot AO\cdot BO}=\frac{100+36-196}{2\cdot10\cdot6}=-\frac{60}{120}=-\frac12\Rightarrow\\AOB=\frac{2\pi}3=120^0$ .

2) (см.рис2) Угол CDO - прямой, т.к. CD - расстояние от вершины С до грани угла (перпендикуляр). Значит, треугольник COD - прямоугольный, CO - гипотенуза. В то же время CO - высота равностороннего треугольника ABC. 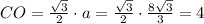$\\CO=\frac{\sqrt3}2\cdot a=\frac{\sqrt3}2\cdot\frac{8\sqrt3}3=4$

Из треугольника COD по определению синуса, синус угла COD равен отношению противолежащего катета CD к гипотенузе CO sinO= 2/4 = 1/2. То есть 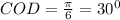$COD=\frac{\pi}6=30^0$

3) (см.рис3) В треугольнике EOF сторона EO - это высота равностороннего трегольника ABE $EO=\frac{\sqrt3}2\cdot AE=\frac{\sqrt3}2\cdot4\sqrt2=2\sqrt6$

Сторона OF равна стороне квадрата, DF равна половине стороны квадрата (OF - средняя линия ABCD), сторону EF найдём из прямоугольного треугольника EFD (EF перпендикуляр к CD => EFD - прямоугольный, ED - гипотенуза): 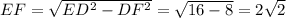$EF=\sqrt{ED^2-DF^2}=\sqrt{16-8}=2\sqrt2$ .

Тогда из треугольника EOF по тереме косинусов:

$\\EF^2=OE^2+OF^2-2\cdot OE\cdot OF\cdot\cos\hat{EOF}\Rightarrow\\\cos\hat{EOF}=\frac{OE^2+OF^2-EF^2}{2\cdot OE\cdot OF}=\frac{24+32-8}{2\cdot2\sqrt6\cdot4\sqrt2}=\frac{48}{16\sqrt{12}}=\frac{48}{32\sqrt3}=\frac{3}{2\sqrt3}=\frac{\sqrt3}2\\\Rightarrow \hat{EOF} = \frac{\pi}6=30^0$

Срисунком в гранях двугранного угла проведены прямые а и b, параллельные его ребру, на расстоянии 10

4,6(14 оценок)

Ответ:

shoistakarimova

07.05.2023

Вели́кие географи́ческие откры́тия — период в истории человечества, начавшийся в XV веке и продолжавшийся до XVII века, в ходе которого европейцы открывали новые земли и морские маршруты в Африку, Америку, Азию и Океанию в поисках новых торговых партнёров и источников товаров, пользовавшихся большим спросом в Европе. Историки обычно соотносят «Великие географические открытия»[1][2] с первопроходческими дальними морскими путешествиями португальских и испанских путешественников в поисках альтернативных торговых путей в «Индии» за золотом, серебром и пряностями[3].

4,4(73 оценок)

Это интересно:

Здоровье

07.12.2021

Повышенная утомляемость во время менструации: причины и способы борьбы...

Компьютеры-и-электроника

31.10.2020

Как быстро и легко поменять свою фотографию обложки на Facebook?...

Семейная-жизнь

29.03.2023

Как развивать в детях творческое начало...

Кулинария-и-гостеприимство