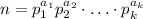, причем это представление единственное с точностью до перестановки множителей (здесь 
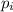- различные простые и 
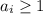). Любой положительный делитель d числа n (включая 1 и само n) имеет такой же вид 
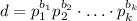, только 
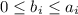. Поскольку каждое 
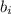может принимать 
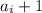значение, то количество делителей числа n равно 
.
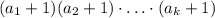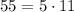, т.е. либо число состоит из одного простого, и тогда 
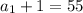, либо число состоит из двух простых, и тогда 
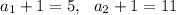. Чтобы число было наименьшим, простые, входящие в его разложение, должны быть минимально возможными, т.е. равны 2 и 3, причем у большего простого должна быть меньшая степень. Таким образом, возможны два варианта для искомого числа: 
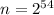или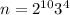 
. Поскольку второе число, очевидно, меньше первого, то ответ 
.
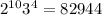