
Первое задание. Первая дробь: 18/28 сокращаешь на 2, получается 9/14
Вторую дробь сокращаешь на 3. Получается 21/27
Второе задание. Чтобы сравнить, нужно привести к общему знаменателю (число под чертой). Под цифрой 1 первую дробь приводим к знаменателю 26,для этого умножаем первую дробь)(6/13) на 2, получаем 12/26. Теперь сравниваем 12/26>11/26
Под цифрой 2 по аналогии, к общему знаменателю (40), умножаем первую дробь на 5,вторую дробь на 8. Получаем 15/40 и 16/40, соответственно вторая дробь больше
Третье задание: 1) общий знаменатель 72,дополнительный множитель для первой дроби 9,для второй 8,получаем 59/72
2)общий знаменатель 24,доп множитель для первой дроби 2,для второй 3,получаем 5/24
3)общий знаменатель 40,дополнительные множители 5 и 4 соответственно, ответ 177/40
4)общий знаменатель 60,дополн множ к первой дроби 6,ко второй 5,ответ 177/60
Четвёртое задание (смотри фото)
Пятое и шестое (смотри фото)
Вроде всё, удачи!
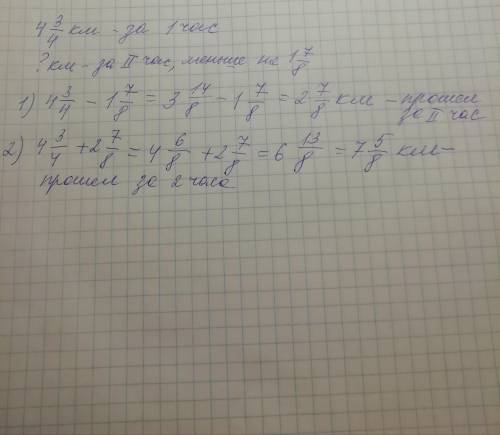

А(18√3; 18)
Пошаговое объяснение:
Координаты точки А будем находить из прямоугольного треугольника, гипотенузой которого будет отрезок ОА=36, первым катетом - отрезок ОВ, лежащий на оси Ох, а вторым катетом - перпендикуляр АВ, опущенный из точки А на ось Ох.
Т.к. угол, который луч OA образует с положительной полуосью Ox
α = 30 °, то катет АВ, лежащий напротив этого угла равен половине гипотенузы ОА, т.е. АВ=ОА:2=36:2=18 (это у - координата точки А).
Найдём длину катета ОВ:
ОВ=√(OA²-AB²)=√(36²-18²)=√972 =18√3 (это х - координата точки А)
Итак, запишем координаты точки А: А(18√3; 18)
y=2x²-2x+1
Пошаговое объяснение:
y=ax²+bx+c
(0;1)-точка пересечения с OY ⇒ x=0 y=1 1=a·0+b·0+c c=1
(1/2 ; 1/2)-вершина параболы x₀=1/2 y₀=1/2
формула для нахождения вершины параболы x₀=-b/2a
-b/2a=1/2 -2b=2a -b=a
y₀=ax₀²+bx₀+1 1/2 = -b(1/2)²+b· 1/2+1
1/2 =-b/4+b/2+1
-1/2=b/4 2b=-4 b=-2 -(-2)=a a=2
y=2x²-2x+1