Во время тренировочных заездов по кольцевой трассе ездят 5 болидов "Формулы-1" на одинаковом расстоянии друг от друга.Каждые 18минут какой то болид пересекает линию старта.Как часто будет пересекаться линия старта,если болидов будет
Пусть C - вершина прямого угла, катет AC равен 20 см, гипотенуза AB равна 25 см. Второй катет (BC) определяем по теореме Пифагора: 25²-20²=(25-20)(25+20)=5*45=25*9=(5*3)²=15² Значит, длина второго катета - 15 см.
Обозначим высоту, проведенную из вершины прямого угла, как CH, причем H - точка на гипотенузе AB. Пусть AH = x (см). Тогда BH = 25-x (см). У нас получилось 2 прямоугольных треугольника: AHC и BHC, в которых H - вершина прямого угла. В этих треугольниках катеты AC и BC являются гипотенузами, катет CH - общий, а другой катет есть выражение от x. Значит, используя теорему Пифагора, можно составить следующее равенство: AC²-AH² = BC²-BH². То есть, мы получили уравнение для x:
Обозначим катеты за a = 9 см, b = 12 см , гипотенузу за c, высоту за h, проекции катетов на гипотенузу за ca и ba.
Исходя из т. Пифагора, следует:
Найдет площадь прямоугольного треугольника:
Воспользуемся формулой площади треугольника через высоту и выразим из нее высоту:
Проекции катетов будут равны:
или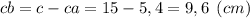
—————————————————————————————
Высоту и проекции катетов также можно найти через пропорциональные отрезки в прямоугольном треугольнике:
– высота, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу:
– катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу:
—————————————————————————————
ответ: гипотенуза равна 15 см, высота — 7,2 см, проекции катетов — 5,4 см и 9,6 см.