F(x) = 2,5x²+15x+22,5
Пошаговое объяснение:
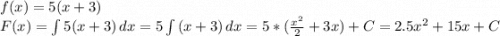
Пускай графики искомых первообразных F(x) пересекают ось абсцисс в точках с координатами (x; 0). x удовлетворяет следующему уравнению:
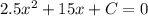
Условие "иметь единственную общую точку" эквивалентно существованию двух совпадающих корней у полученного квадратного уравнения. Это бывает тогда и только тогда, когда дискриминант равен нулю.
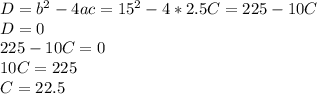
Получили, что F(x) = 2,5x²+15x+22,5 — единственная первообразная заданной функции, которая имеет единственную общую точку с осью абсцисс.
x ∈ ( 0; 1) <возрастание>
Пошаговое объяснение:
Дано: y = 1 + 3x² - 2x³
Найдем производную:
y' = (1 + 3x² - 2x³)' = 0 + 3*2x²⁻¹ - 2*3x³⁻¹ = 6x - 6x²
Приравняем к нулю и (решая соответственно уравнение) найдем критические точки (корни полученного уравнения):
6x - 6x² = 0
-6x (x - 1) = 0
x₁ = 0 x₂ = 1 <критические точки>
Выводим на числовую ось (самостоятельно, так как возможности печати набор символов ограничен)
Находим участки возрастания и убывания:
x ∈ (-∞; 0) ∪ (1; +∞) <убывание>
x ∈ ( 0; 1) <возрастание>
В решении.
Пошаговое объяснение:
Построить графики. Графики линейной функции, прямые линии. Придать значения х, подставить в уравнение, вычислить у, записать в таблицу. Для построения прямой достаточно двух точек, для точности построения определить три.
Прежде преобразовать уравнения в уравнения функций:
х+у-3=0 2х-у-4=0 х+4у-3=0 3х+у-2=0 х+9=0 4у+8=0
у=3-х -у=4-2х 4у=3-х у=2-3х х= -9 4у= -8
у=2х-4 у=(3-х)/4 у= -8/4
у=0,75-0,25х у= -2
Таблицы:
у=3-х у=2х-4 у=0,75-0,25х у=2-3х
х -1 0 1 х -1 0 1 х -1 3 7 х -1 0 1
у 4 3 2 у -6 -4 -2 у 1 0 -1 у 5 2 -1
х = -9 прямая, параллельная оси Оу, проходит через точку х= -9;
у = -2 прямая, параллельная оси Ох, проходит через точку у= -2.
(х = -9 сами достройте, вертикальная линия, проходит через х= -9 и параллельна оси Оу).