Question

В уравнении x2 + p1/2x + q = 0 значения p ∈ [0, 1] и q ∈ [-1, 1]. Выбор p и q абсолютно случайный и независимый. Найдите вероятность того, что уравнение имеет хотя бы один действительный корень.

Answer 1

если x2 + p1/2x + q = 0 это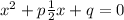 $x^2+p\frac{1}{2} x+q=0$ то

$x^2+p\frac{1}{2} x+q=0\\D=(\frac{1}{2}p )^2-4q\geq 0\\\frac{p^2}{4} -4q\geq 0\\p^2-16q\geq 0\\p^2\geq 16q\\$

Если q [-1;0] то уравнение всегда имеет хотя бы один корень.

р в среднем 1/2 то q должно быть не больше 1/64.

Получается нам не подходят случаев 63/128

А подходят 65/128 = 50,78125%