Question

Решите данную задачу с функции Эйлера

Answer 1

799

Пошаговое объяснение:

 Приведем сначала необходимую теорию. Функция Эйлера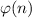 $\varphi(n)$ вычисляет количество натуральных чисел, меньших натурального числа n и взаимно простых с n. Ясно, что если n - простое число, то

$\varphi(|n)=n-1.$ Менее очевидный факт (доказывать его мы не будем) состоит в том, что если натуральные числа m и n взаимно просты, то

                                        $\varphi(mn)=\varphi(m)\cdot \varphi(n).$

И, наконец,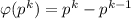 $\varphi(p^k)=p^k-p^{k-1}$ при простом p и натуральном k.

Дальше всё просто. Сосчитаем функцию Эйлера при n=2020, разложив 2020 на простые множители:

    $\varphi(2020)=\varphi(4\cdot 5\cdot 101)=\varphi(2^2) \varphi(5)\varphi(101)= (2^2-2^1)(5-1)(101-1)=800.$

Итак, мы имеем ровно 800 натуральных чисел, меньших 2020, взаимно простых с 2020. А нас спрашивают, сколько натуральных чисел от 1 до 2018 взаимно просты с 2020. Поскольку два соседних натуральных числа не имеют общих множителей (кроме 1), 2019 взаимно просто с 2020. Поэтому ответом в задаче служит число 800-1=799.