(3х2 - 5х + 3) + (-3х2 - 7х) = 27
(6 - 5х + 3) + (-6 - 7х) = 27
Раскрываем скобки.Перед первой скобкой ничего не стоит,значит это плюс.А раз плюс просто переписываем.У второй точно так же.
6-5х+3+(-6) - 7х = 27
Приведём подобные слагаемые.В данном случае это 6, +3,-6. 6 и -6 противоположные числа и в сумме дают 0 Получаем:
-5х+3 - 7х = 27
Всё,что с буквами (х) должно быть слева.А всё,что без букв (х) вправо,при этом поменяв на противоположные знаки.
-5х-7х=27-3
-35х=24
х=24:(-35)
х= - 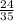
ответ: - 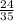
КОМУ НАДО БЫСТРО:
(3х2 - 5х + 3) + (-3х2 - 7х) = 27
(6 - 5х + 3) + (-6 - 7х) = 27
6-5х+3+(-6) - 7х = 27
-5х+3 - 7х = 27
-5х-7х=27-3
-35х=24
х=24:(-35)
х= - 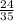
ответ: - 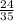
Пошаговое объяснение:
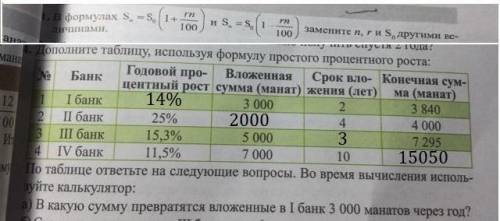
Формула простого процента общая для всех случаев S=S₀*(1+rn/100)
1) S=3840, S₀=3000, n=2, r=?
3840=3000*(1+(r*2/100)
3000+60r=3840
60r=840
r=840:60
r=14% годовых
2) S = 4000, r=25%. n=4, S₀=?
4000=S₀*(1+25*4/100)
S₀*(1+1)=4000
S₀=4000:2
S₀=2000 манат первоначальная сумма вклада
3) S₀=5000, S=7295, r=15,3%, n=?
7295=5000*(1+15,3*n/100)
5000+50*15,3n=7295
765n=2295
n=2295:765
n=3 года срок вклада
4) S₀=7000, r=11,5%, n=10 лет , S=?
S= 7000*(1+11,5*10/100)=7000+70*11,5=7000+8050=15050 манат , конечная сумма
таблица во вложении
Пошаговое объяснение: Докажем более сильное утверждение: если p - нечетное число, не кратное трем, то p²-1 кратно 24.
Докажем более сильное утверждение: если p - нечетное число, не кратное трем, то p²-1 кратно 24.
А для этого докажем такое утверждение: произведение
p³-p=(p-1)p(p+1)
трех последовательных целых чисел, среднее из которых нечетное, кратно 24. Это утверждение следует из того, что 24=3·8, из того, что одно из трех последовательных чисел обязательно делится на 3, а также из того, что оба крайних числа четные, а одно из них даже делится на 4.
Переходим к доказательству утверждения про p²-1 =(p-1)(p+1)
при нечетном p, не делящимся на 3. Предыдущее утверждение гарантировало делимость на 24 произведения (p-1)p(p+1), но поскольку в нашем случае p не делится на 3, на три делится p-1 или p+1. Делимость на 8 также обеспечивали крайние числа.
И, наконец, если p - простое число большее 3, оно нечетное и не делится на 3, поэтому к нему можно применить только что доказанное утверждение.