Question

Найти производные y' =dy/dx заданных функций

Answer 1

Пошаговое объяснение:

б) $\[{\mathop{\rm tg}\nolimits} y = xy + \ln xy;\]$

Подразумеваем, что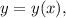 $y = y(x),$ дифференцируем обе части по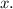 $x.$

Так,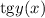 ${\mathop{\rm tg}\nolimits} y(x)$ — сложная функция, поэтому ее производная это сперва производная от тангенса, умноженная на производную от его аргумента $(y(x))$: $({\mathop{\rm tg}\nolimits} y(x))' = \frac{1}\cos }^2}y}} \cdot y'.$

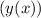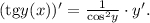
Находим производную xy как производную произведения: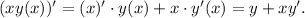 $(xy(x))' = (x)' \cdot y(x) + x \cdot y'(x) = y + xy'.$

Производная логарифма — опять сложная функция: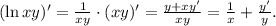 $(\ln xy)' = \frac{1}{{xy}} \cdot (xy)' = \frac{{y + xy'}}{{xy}} = \frac{1}{x} + \frac{{y'}}{y}.$

Вместе получаем: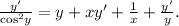 $\frac{{y'}}\cos }^2}y}} = y + xy' + \frac{1}{x} + \frac{{y'}}{y}.$

Выражаем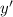 $y'$ из последнего равенства. Можно преобразовать ответ, избавившись от «двухэтажных» дробей: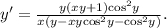 $y' = \frac{{y(xy + 1){{\cos }^2}y}}{{x(y - xy{{\cos }^2}y - {{\cos }^2}y)}}.$

в)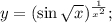 $y = {(\sin \sqrt x )^{\frac{1}{{{x^2;$

Прологарифмируем по натуральному основанию обе части данного равенства: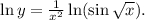 $\ln y = \frac{1}{{{x^2}}}\ln (\sin \sqrt x ).$ Теперь найдем производную от обеих частей аналогично решению п. б).

$\frac{{y'}}{y} = - \frac{2}{{{x^3}}}\ln (\sin \sqrt x ) + \frac{1}{{{x^2}}} \cdot \frac{1}{{\sin \sqrt x }} \cdot \cos \sqrt x \cdot \frac{1}{{2\sqrt x }};\\$

$\frac{{y'}}{y} = \frac{{\sqrt x {\mathop{\rm ctg}\nolimits} \sqrt x - 4\ln (\sin \sqrt x )}}{{2{x^3}}};\\$

$y' = y \cdot \frac{{\sqrt x {\mathop{\rm ctg}\nolimits} \sqrt x - 4\ln (\sin \sqrt x )}}{{2{x^3}}};\\$

$y' = \frac(\sin \sqrt x )}^{\frac{1}{{{x^2{{2{x^3}}} \cdot (\sqrt x {\mathop{\rm ctg}\nolimits} \sqrt x - 4\ln (\sin \sqrt x )).\\$