Уравнение трехзначного числа: 100a+10b+c, где a - число сотен, b - число десятков и x - число единиц. Сумма цифр такого числа равна a+b+c. 100a+10b+c+7 (a+b+c) = 1000 107a+17b+8c=1000. При b=c=0 получим 107a=1000, и тогда a=9. При b=c=9 получим 107a+153+72=1000; 107a=775, получается a=7. При a=7: 749+17b+8c=1000; 17b+8c=251; При b=c=9 получим 225≠251, следовательно, a≠7. При a=8 получаем 856+17b+8c=1000; 17b+8c=144; b = (144-8c) / 17, c в промежутке между 0 и 9. Так как это число натуральное, подбираем такое с, чтобы дробь была целой. При с=1 и получаем b = 8. Это число 887. ответ: 887.
Пошаговое объяснение:
Задумано число 32 или 56.
Пошаговое объяснение:
Пусть задумано число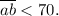 Тогда по условию
Тогда по условию
Так как по условию задачи число меньше 70, то его первая цифра меньше 7, значит
Поскольку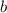 цифра,
цифра, 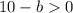 и на это выражение можно умножить обе части неравенства.
и на это выражение можно умножить обе части неравенства.
То есть «кандидаты» в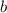 должны, с одной стороны, быть из диапазона от 1 до 7, а с другой число
должны, с одной стороны, быть из диапазона от 1 до 7, а с другой число 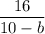 должно быть целым. Перебором убеждаемся, что подходят
должно быть целым. Перебором убеждаемся, что подходят 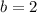 или
или 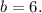 Тогда
Тогда
Искомые числа — 32 или 56.