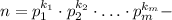 разложение n на простые множители. Каждый делитель числа n имеет подобный вид с теми же основаниями и с показателями от 0 до степени, в которую это простое число входит в разложение числа n. Поэтому n имеет
разложение n на простые множители. Каждый делитель числа n имеет подобный вид с теми же основаниями и с показателями от 0 до степени, в которую это простое число входит в разложение числа n. Поэтому n имеет 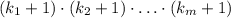 делителей. Но по условию n имеет 15 делителей. Это приводит к двум случаям.
делителей. Но по условию n имеет 15 делителей. Это приводит к двум случаям.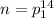 . Этот случай нас не устраивает, так как это число больше, чем 300.
. Этот случай нас не устраивает, так как это число больше, чем 300.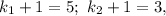 то есть
то есть 
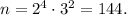
 и так далее, больше, чем 300.
и так далее, больше, чем 300.
Для решения данной задачи нам нужно сложить два смешанных числа. Давайте приведем оба числа к неправильной дроби и затем выполним сложение.
1 3/7 = (7 * 1 + 3) / 7 = 10 / 7
8 4/7 = (7 * 8 + 4) / 7 = 60 / 7
Теперь сложим полученные дроби:
10 / 7 + 60 / 7 = (10 + 60) / 7 = 70 / 7 = 10
Таким образом, ответ на вашу задачу равен 10. Вариант ответа Б-17,23 не является правильным, а правильный ответ - 10 (ответ Г-0,723) в предложенных вариантах ответа.
Пошаговое объяснение: