Что мы будем использовать: последовательность 
монотонно возрастает и имеет конечный предел; этот предел обозначается буквой e. Первые цифры числа e все знают. Для нас достаточно знать, что
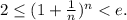
1) 
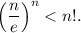При n=1 неравенство очевидно. Предположим, что оно справедливо при некотором n, и докажем, что тогда оно справедливо при n+1. Итак, нужно доказать, что 
Имеем:
2) 
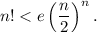При n=1 неравенство очевидно. Предположив, что при некотором n неравенство справедливо, докажем, что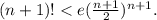 
Имеем:
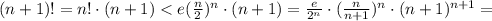
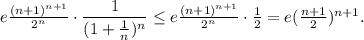
Доказательство завершено благодаря тому, что все натуральные числа расположены "по порядку" одно за другим, и есть первое натуральное число (принцип домино: если доминошки расположить на боку одну рядом с другой на небольшом расстоянии друг от друга в виде змеи, и уронить первую доминошку на вторую, то вторая упадет на третью, третья на четвертую и так далее, пока не упадут все).
Пошаговое объяснение:
1.
375 : 3 - площадь 2-го участка
375 - 375 : 3 - разность площадей 1-го и 2-го участков
375 + 375 : 3 - сумма площадей 1-го и 2-го участков
(375 + 375 : 3) · 2 - площадь 3-го участка
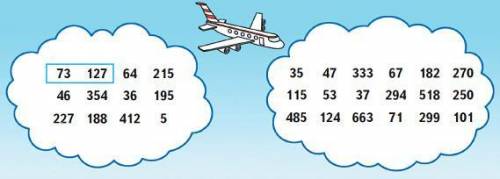
2. Пары чисел, сумма которых круглое число:
1-е облако: 73 и 127; 64 и 36; 354 и 36; 46 и 354; 215 и 195; 195 и 5; 188 и 412
2-е облако: 35 и 115; 47 и 53; 47 и 333; 333 и 37; 115 и 485; 53 и 37; 333 и 67; 37 и 663; 182 и 518; 270 и 250; 299 и 101; 71 и 299.
3.
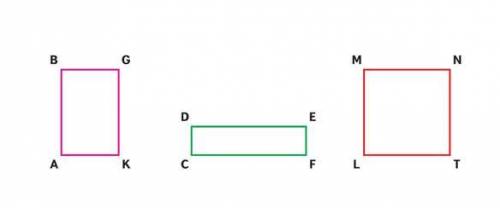
Названия прямоугольников: розовый - ABGK; зелёный - CDEF; красный - LMNT. Наибольший периметр имеет прямоугольник LMNT
60 дер, 20 дер.
Пошаговое объяснение:
Нехай на одній ділянці 3х дерев, а на другій - х. Тоді коли з першої вивезли 30 дерев, стало 3х-30 дер. Коли на другу посадили 10 дерев, стало х+10 дер. Так як дерев стало порівну, то:
3х-30 = х+10
3х-х = 10+30
2х = 40
х = 20
Отже, на другій ділянці було 20 дерев, а на першій 20*3=60 дерев.