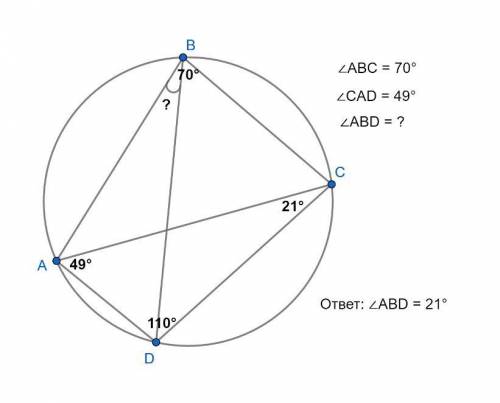
∠ABD = 21°.
Пошаговое объяснение:
Рисунок прилагается.
Если четырехугольник вписан в окружность, то сумма его противолежащих углов равна 180°.
∠ABC + ∠ADC = 180° ; ∠ABC = 70° по условию.
∠ADC = 180° - ∠ABC = 180° - 70° = 110°;
Сумма углов треугольника = 180°. В ΔCAD ∠CAD = 49° по условию, ∠ADC = 110°; ∠ACD = 180° - ∠CAD - ∠ADC = 180° - 49° - 110° = 21°.
Вписанные углы, опирающиеся на одну и ту же хорду окружности, равны между собой.
∠ABD и ∠ACD вписанные углы, опирающиеся на одну хорду AD.
∠ABD = ∠ACD = 21°.
ответ: 1.124 кв. ед.
Пошаговое объяснение:
f(x) = x^2;
g(x) = 1-x^2;
По формуле Ньютона-Лейбница
S=∫ₐᵇg(x)dx - ∫ₐᵇf(x)dx = G(x)|ₐᵇ - F(x)|ₐᵇ.
Строим графики функций (см. скриншот) и находим пределы интегрирования => a=-0.707; b=0.707. Тогда
S=S(ABmCD) - S(ABnCD) = ∫ₐᵇg(x)dx - ∫ₐᵇf(x)dx=∫ₐᵇ(1-x^2)dx - ∫ₐᵇ(x^2)dx =
1) ∫ₐᵇ(1-x^2)dx = ∫ₐᵇ1dx - ∫ₐᵇ(x^2)dx = x|ₐᵇ - x^3/3|ₐᵇ = 0.707-(-0.707) = 1.414;
2) ∫ₐᵇ(x^2)dx = x^3/3|ₐᵇ = 1/3(0.707^3 - (-0.707^3)) = 1/3 (0.35 -(-0.35)) =
= 1/3 *0.7 = 0.23 кв. ед.
S = 1,414 - 0,23 = 1.124 кв. ед.