вынести за скобку:
24(-5+14) = (-5)*24+ 14*24 = 9*24= 216;
-15(4-15) = -60*(-225) = 13500 ;
21(-4-9) = -89*(-189) = 15876;
-3(-8-4) = -3(-8) + (-3)*(-4)= 12+24= 36;
(24+25)*(-4) = (-4)*24+(-4)*25= -196;
найти общий множитель:
1) 37*29+29*143 = 29(37+143) = 29*180= 5220;
2) 367*24 + 367*76 = 367(24+76)= 367*100 = 36700;
3) 289*129 - 289*24 = 289 (129-24) = 284*105 = 29820;
4) 19*24+24*151 + 170*6 = 456 + 3624 + 1020 = 5100;
5) -15*24-17*15 = 15(-24-17) = 15(-41) = -615;
6) 143*(-672) - 678*(-143) = (-143)*672+678*143= 143*(-6)*(112-113) = 143* (-6)*(-1) = 858;
7) 19* 876 - 67* (-19) = 19*876 + 67*19 = 19(876 +67) = 19*43 = 17917;
8) 5400 - 54*99 = 5400 - 2106 = 3294;
9)777 * 156 +156 = 156*(777+1) = 157*778 = 121368;
10)888*888 - 888*889 - 8880 =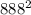 
- 888*889 - 8880 = 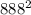- 798312 = - 9768;
ответ: a = 28
Пошаговое объяснение:
a : 2 целых 3/23 = 3 целых 2/7 : 1/4;
a/((2 * 23 + 3)/23) = ((3 * 7 + 2)/7)/(1/4);
a/((46 + 3)/23) = ((21 + 2)/7)/(1/4);
a/(49/23) = (23/7)/(1/4);
a * 23/49 = 23/7 * 4;
a * 23/49 = 23 * 4/7;
a = (23*4/7)/(23/49);
a = 23*4/7 * (49/23);
Числитель и знаменатель в дроби в правой части выражения сокращаем на 23, тогда получим:
a = 1*4/7 * (49/1);
a = 4/7 * 49;
Числитель и знаменатель в дроби в правой части выражения сокращаем на 7, тогда получим:
a = 4/1 * 7;
a = 4 *7;
a = 28.
За умовою маємо AOC = 120 градусів.
Оскільки сума кутів у трикутнику дорівнює 180 градусів, маємо BOC = 180 - AOC = 60 градусів.
За умовою також маємо співвідношення AOB : BOC = 1:5.
Нехай AOB = x, тоді BOC = 5x.
За теоремою синусів для трикутника АОВ маємо:
sin120/sinx = OA/OV
Оскільки OA = OV, то sin120/sinx = 1.
Отже, sinx = sin120 = √3/2.
Так як 0 < x < 180, маємо два можливих значення для x: x = 60 або x = 120.
Якщо x = 60, то AOB:BOC = 1:5, а ОАВ + ВОС + СОА = 180°, тоді ОАВ = 60°, а ОВС = СОА = 60°.
Отже, ми маємо трикутник з кутами 60°, 60° та 60°, який є правильним трикутником. Тоді АOB = BOC = 60 градусів.
Якщо x = 120, то AOB:BOC = 1:5, а ОАВ + ВОС + СОА = 180°, тоді ОВС = 60°, а ОАВ = СОА = 60/2 = 30°.
Отже, ми маємо трикутник з кутами 30°, 60° та 90°, де кут між А та О дорівнює 30 градусам, тоді АOB = 90°/2 = 45°, а БОС = 60° - 45° = 15°.
Отже, відповідь: AOB дорівнює 60 градусів або 45 градусів.