пусть x кг муки было первоначально в другом мешке; тогда пусть в первом мешке было первоначально 3x кг муки; по условию в другом мешке стало после первоначально (x+2) кг муки; также в первом мешке стало после первоначально (3x-4) кг муки.
учитывая все условия, составим уравнение и решим эту задачу алгебраическим
если в другом мешке было первоначально 3 кг муки, то в первом мешке первоначально было 3x=3*3=9 кг муки.
проверка: 3*3-4=9-4=5 кг муки стало после первоначально в первом мешке; 3+2=5 кг муки стало после первоначально в другом мешке.
ответ: в первом мешке было первоначально 9 кг муки, а в другом 3 кг муки было первоначально.
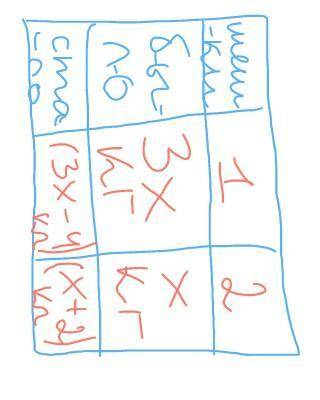
пусть x кг муки было первоначально в другом мешке; тогда пусть в первом мешке было первоначально 3x кг муки; по условию в другом мешке стало после первоначально (x+2) кг муки; также в первом мешке стало после первоначально (3x-4) кг муки.
учитывая все условия, составим уравнение и решим эту задачу алгебраическим
если в другом мешке было первоначально 3 кг муки, то в первом мешке первоначально было 3x=3*3=9 кг муки.
проверка: 3*3-4=9-4=5 кг муки стало после первоначально в первом мешке; 3+2=5 кг муки стало после первоначально в другом мешке.
ответ: в первом мешке было первоначально 9 кг муки, а в другом 3 кг муки было первоначально.

ответ и Пошаговое объяснение:
Перевод: Постройте график функции y = 3–0,5·x. Определите координаты точек, в которых её график пересекает оси координат.
Решение. График линейной функции y = 3–0,5·x - эта прямая. Для построения графика прямой достаточно 2 точки, через которые проходит эта прямая. Находим эти точки из уравнения функции (красные точки):
1) x=2 ⇒ y= 3–0,5·2 = 3–1 = 2 ⇒ (2; 2);
2) x=4 ⇒ y= 3–0,5·4 = 3–2 = 1 ⇒ (4; 1).
График в приложенном рисунке. Из рисунка определяем, что координаты точки пересечения графика функции с осью Ох – эта (6; 0) и координаты точки пересечения графика функции с осью Оу – эта (0; 3).
#SPJ1