а) 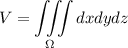 . В нашем случае
. В нашем случае 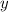 меняется от
меняется от 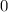 до
до 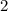 ,
,  меняется от
меняется от 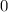 до
до 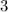 , а
, а  заключен между
заключен между 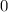 и
и 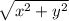 . По сути
. По сути  можно представлять себе как множество отрезков высоты
можно представлять себе как множество отрезков высоты 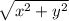 выпущенных из точки
выпущенных из точки 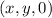 , причем эти точки берутся из прямоугольника
, причем эти точки берутся из прямоугольника ![[0,2]\times [0,3]](/tpl/images/4758/9834/e2d7a.png) .
.
Итак, 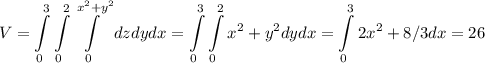 .
.
б) Здесь рассуждения такие же, только  представляет собой не прямоугольник, а область, ограниченную двумя <<перпендикулярными>> параболами на плоскости
представляет собой не прямоугольник, а область, ограниченную двумя <<перпендикулярными>> параболами на плоскости 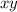 . Величина
. Величина  будет меняться от
будет меняться от 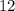 до минимального значения на
до минимального значения на  , что соответствует максимуму
, что соответствует максимуму 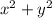 на
на  -- то есть макисмальному удалению от начала координат. Это происходит в точке пересечения парабол -- точке
-- то есть макисмальному удалению от начала координат. Это происходит в точке пересечения парабол -- точке 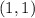 (а начало координат не подходит). Значит,
(а начало координат не подходит). Значит, 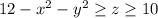 . Итого:
. Итого: 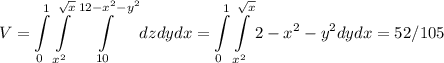 .
.
в) Здесь удобно сделать замену координат: 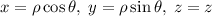 , тогда поверхности:
, тогда поверхности: 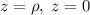 . Якобиан
. Якобиан 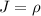 , имеем:
, имеем: 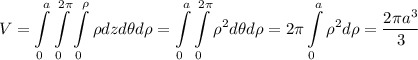 .
.
1. Вместо с могут быть цифры 2, 5, 8
2. Вместо b может быть только цифра 7
Пошаговое объяснение:
1) Дано число 79с. Какая цифра должна быть вместо с, чтобы дан- ное число было кратно числу 3?
Число делится на 3 тогда и только тогда, когда сумма его цифр делится на 3:
7 + 9 + с = 16 + с = 16 + 2 = 18 - сумма делится на 3 - 792
7 + 9 + с = 16 + с = 16 + 5 = 21 - сумма делится на 3 - 795
7 + 9 + с = 16 + с = 16 + 8 = 24 - сумма делится на 3 - 798
2) Дано число 5b6. Какая цифра должна быть вместо , чтобы дан- ное число было кратно числу 9?
На 9 делятся только те числа, сумма цифр которых делится на 9:
5 + b + 6 = 11 + b = 11 + 7 = 18 - сумма делится на 9 - 576
Пошаговое объяснение:
⎣
2
3
1
2
−
3
−
3
4
−
2
3
⎤
⎥
⎦
⎡
⎢
⎣
x
y
z
⎤
⎥
⎦
=
⎡
⎢
⎣
10
22
−
2
⎤
⎥
⎦
Find the determinant of the coefficient matrix
⎡
⎢
⎣
2
3
1
2
−
3
−
3
4
−
2
3
⎤
⎥
⎦
.
Нажмите для увеличения количества этапов...
D
=
−
76
Since the determinant is not
0
, the system can be solved using Cramer's Rule.
Find the value of
x
by Cramer's Rule, which states that
x
=
D
x
D
.
Нажмите для увеличения количества этапов...
x
=
5
Find the value of
y
by Cramer's Rule, which states that
y
=
D
y
D
.
Нажмите для увеличения количества этапов...
y
=
2
Find the value of
z
by Cramer's Rule, which states that
z
=
D
z
D
.
Нажмите для увеличения количества этапов...
z
=
−
6
Приведем решение системы уравнений.
x
=
5
y
=
2
z
=
−
6