ответ: 22,5 км/ч.
Пошаговое объяснение:
Пусть s (км) и t (ч) - путь и время, за которое проехал его мопед, тогда средняя скорость мопеда v=s/t (км/ч). Пусть t1, t2 и t3 - время, за которое мопед проехал соответственно 30% пути, 10% пути и оставшуюся часть пути. Тогда t=t1+t2+t3, причём t1=0,3*/v1, t2=0,1*s/v2 и t3=0,6*s/v3, где v1=27 км/ч, v2=30 км/ч, v3=20 км/ч. А так как t=s/v, то отсюда следует уравнение s/v=0,3*s/27+0,1*s/30+0,6*s/20. Сокращая обе части на s, получаем уравнение 1/v=0,3/27+0,1/30+0,6/20=40/900=2/45, откуда v=45/2 =22,5 км/ч.
0,6
Пошаговое объяснение:
Количество двузначных чисел от 10 до 99 составляет 90.
Числа, которые делятся на 2, это числа которые оканчиваются цифрами 0, 2, 4, 6 или 8.
Числа, которые делятся на 5, это числа которые оканчиваются цифрой 0 или 5.
Числа, которые делятся на 2 и 5, это числа которые оканчиваются цифрой 0.
Таким образом, среди каждого десятка двузначных чисел количество чисел, которые подходят под критерии, а именно оканчиваются на одну из цифр 0, 2, 4, 5, 6, 8, составляет 6 штук. Например, в десятке чисел от 30 до 39, на 2 делятся 30, 32, 34, 36, 38, а на 5 делится 35, и на 2 и 5 делится 30, то есть подходящие под нужный критерий числа - это числа 30, 32, 34, 35, 36, 38, всего 6 штук.
Так как всего двузначных чисел 90, то есть 9 десятков, то подходящих чисел будет 9*6 = 54.
По классическому определению вероятности, вероятность того , что наудачу взятое двухзначное число окажется кратным либо 2, либо 5, либо тому и другому одновременно составляет 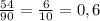
91=90+1
77=70+7
36=30+6
42=40+2
54=50+4
3 десятка и 2 единицы- это 32, а 12 единиц- это 12 => 32-12=20 - это 2 десятка и 0 единиц