Математика: По текст на тему на уроці німецької мови

По текст на тему на уроці німецької мови

👇

Ответ:

димас203

06.06.2022

In der Deutschstunde Die Sprache ist das wichtigste Mittel der Verständigung unter den Menschen.In der Schule lernen wir Deutsch.Unsere Deutschlererin heißt Switlana Iwaniwna.Sie unerrichtet Deutsch bei uns schon 3 Jahre lang.Zuerst prüfen wir die Hausaufgabe.Wir lesen den Text und übersetzen ihn.Einer der Schüler beantwortet die Fragen.Ubekannte Wöreter schreiben wir ins Vokabelheft heraus.Danach üben wir die Aussprache.Die Lehrerin liest die Sätze und wir wiederholen sie.Dann machen wir eine Übung.Sie ist schwer.Die Lehrerin erklärt uns unbekannte Stellen.Zuletzt führen wir das Dialog zum Thema:"Mein Lieblingsfach".Switlana Iwaniwna stellt uns die Noten.Ich bekomme eine 10.Die Stunde ist aus.

4,6(42 оценок)

Открыть все ответы

Ответ:

teXerStas

06.06.2022

26 тонн

Пошаговое объяснение:

вся работа была выполнена за 11 дней, значит число n=11. Так как масса всего щебня равна 176, то это число является суммой нашей прогрессии, т.е. S11=176. Требуется найти, сколько тонн было перевезено в последний день, а он – 11, значит, найти надо а11.

Итак, если нам встретилась сумма арифметической прогрессии, значит, нам надо воспользоваться формулой суммы n первых членов арифметической прогрессии Sn=а1+аn2∙n, куда мы и подставим все данные: 176=6+а112∙11.

Разделим обе части на 11, получим 16= 6+а112 ; умножим 16 на 2 (правило пропорции): 32=6+а11. Отсюда найдем а11=32–6=26. Итак, мы нашли, что 26 тонн щебня было перевезено в последний день.

ответ: 26

4,7(20 оценок)

Ответ:

daaler

06.06.2022

$\max f(x \in[0;\;\pi] ) = f(0) = \frac{4}{3} \\ \min f(x \in[0;\;\pi] ) = f(\pi) = - \frac{4}{3}$

Пошаговое объяснение:

$f(x) = \cos{x} + \frac{1}{3} \cos(3x) \\ \max f(x \in[0;\;\pi] )$

Функция непрерывна и определена на R, а следовательно и на всем заданном отрезке.

Максимальное значение f(x) на отрезке может быть:

- на концах заданного отрезка

- в точках экстремума функции.

Т.е. следует проверить значения функции в точках

1) где f'(x)=0

2) х = 0; х = П

1) Найдем производную f'(x)

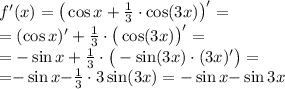
$f'(x) = \big(\cos{x} + \frac{1}{3} \cdot\cos(3x)\big)'= \\ = (\cos{x})' + \frac{1}{3} \cdot\big(\cos(3x)\big)'= \\ = - \sin{x }+ \frac{1}{3} \cdot\big( - \sin(3x)\cdot(3x)' \big) = \\ { = } {-} \sin{x }{ - } \frac{1}{3} \cdot 3\sin(3x) = - \sin{x }{ - }\sin{3x }$

Найдем нули производной:

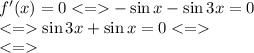
$f'(x)=0 - \sin{x } - \sin{3x } =0 \\ \sin{3x } + \sin{x } =0 < = \\ < =$

Применим формулу

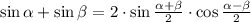
$\sin \alpha + \sin \beta = 2\cdot \sin \frac{ \alpha + \beta }{2}\cdot\cos \frac{ \alpha - \beta }{2}$

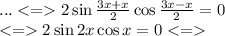
$... 2\sin \frac{3x + x}{2} \cos \frac{3x - x}{2} =0 \\ < = 2\sin2x \cos{x} = 0 < = \\$

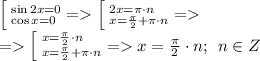
$\Big[ \: \Large{^{}_{}} ^{\sin2x = 0}_{\cos{x} = 0} = \Big[ \: \Large{^{}_{}} ^{2x = \pi\cdot{n}}_{{x} = \frac{\pi}{2} +\pi\cdot{n} } = \\ = \Big[ \: \Large{^{}_{}} ^{x = \frac{\pi}{2} \cdot{n}}_{{x} = \frac{\pi}{2} +\pi\cdot{n} } = \small{x = \frac{\pi}{2} \cdot{n};\: \: n \in Z}$

При

$x \in[0;\;\pi] \\0 \leqslant x = \frac{\pi}{2} \cdot{n} \leqslant \pi \\ 0 \leqslant \frac{n}{2} \leqslant 1 \\ 0 \leqslant {n} \leqslant 2 = n \in \: \{0;\;1;\;2 \} \\ x = \{0;\; \frac{\pi}{2} ;\;\pi\}$

Проверим точки: (кстати, концы отрезка также входят в точки экстремума функции)

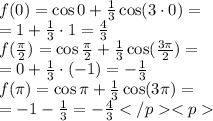
$f(0) =\cos{0} + \frac{1}{3} \cos(3 \cdot0) = \\ = 1 + \frac{1}{3} \cdot1 = \frac{4}{3} \\ f( \frac{\pi}{2}) = \cos{ \frac{\pi}{2} } + \frac{1}{3} \cos( \frac{3\pi}{2} ) = \\ = 0 + \frac{1}{3} \cdot( - 1) = - \frac{1}{3} \\ f(\pi) = \cos{\pi} + \frac{1}{3} \cos(3 \pi) = \\ = - 1 - \frac{1}{3} = - \frac{4}{3}$