Пусть масса абрикоса равняется х г, масса лимона - у г, а масса апельсина - z г.
x+y+z=270.
Попытаемся избавиться от лишних переменных.
1 лимон весит как 3 абрикоса, т.е. у=3х, значит у мы можем заменить на 3х.
1 апельсин весит как 5 абрикосов, т.е. z=5х. Заменим переменную z на 5х.
В итоге у нас получается:
х+3х+5х=270
9х=270
х=270/9
х=30.
30 грамм весит 1 абрикос.
Ранее мы выяснили, что 1 апельсин = 5 абрикосов.
т. е. 1 апельсин (z) = 5х
z = 5x
z = 5*30
z = 150.
Значит, 1 апельсин весит 150 грамм.
ответ: 150 г
Для начала упростим саму функцию:
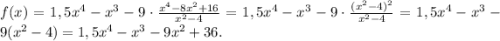
Отмечу, что сокращать дробь можно только в том случае, когда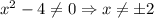 
.
Ищем производную:
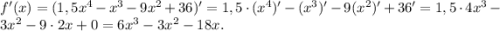
Найдем критические точки - точки, в которых производная равна 0 или не существует. Последних у нас нет, т.к. значения выражения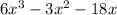 
можно вычислить при любом иксе. Значит, остается только приравнять его к 0:
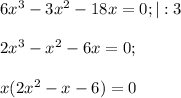
Произведение равно 0, когда хотя бы один множитель равен 0. Т.е. или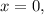 
или 
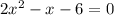. Заметим, что корнем второго уравнения является число 
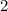. Тогда по теореме Виета второй корень равен 
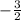(поскольку для уравнения 
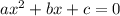по все той же теореме Виета
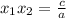. В нашем случае 
. В итоге, подставляя числа, получаем: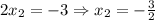 
).
Итого имеем 3 крит. точки: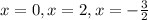 
. Вспоминаем про то, что 
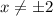и отбрасываем вторую точку. Остаются только 2: 
.
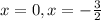Если x < -3/2, то значение производной < 0; если x є (-3/2; 0), то значение производной > 0. Т.е. при переходе через точку x = -3/2 знак производной меняется с минуса на плюс, а значит точка x = -3/2 является точкой минимума функции.
ОТВЕТ: -3/2.
1) кладём по 3 монетки на каждую чашу, монеты из чаши, что опустилась ниже, убираем;
2) Из оставшихся монет выбираем 2 и кладём по 1 на весы, далее 2 варианта:
1. Чаши на одном уровне, фальшивка у вас в руке
2. Чаши на разном уровне, фальшивка та, что на чаше выше.