Предположим, что весь центр куба 4х4х4 состоит из черных кубиков.
Тогда из них будет составлен куб 2х2х2 то есть всего - 8 кубиков.
Осталось: 32 - 8 = 24 черных кубика.
Минимальное количество черных плоскостей, размером 1х1 будет при расположении черных кубиков в центре каждой грани.
Всего в кубе 6 граней. Центр каждой составляет квадрат 2х2. То есть 4 черных квадратика в центре каждой грани. Всего 24.
Если мы сместим хотя бы один черный кубик на ребро или в угол куба, то количество черных квадратиков увеличится на 1 и на 2 соответственно.
Таким образом, минимальное количество черных квадратиков на поверхности данного куба - 24.
Так как каждая грань состоит из 16 квадратиков, то всего таких квадратиков на поверхности куба: 16 · 6 = 96.
Вычтем черные квадратики: 96 - 24 = 72 (белых квадратика 1х1)
ответ: 72.
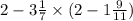
Сначала для удобства переведём дроби в неправильные:
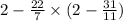
Теперь поочерёдно начнём выполнять действия. Первым действием является скобка. Перед тем, как выполнить вычитание, нужно привести оба числа в одинаковому знаменателю, для этого умножим 2 на 11 и после этого вычтем:
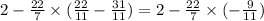
Следующим действием является умножение. Обе дроби являются отрицательными, значит их произведение будет положительным, так как при умножении минуса на минус бужет плюс. Сократим и умножим:
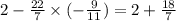
Осталось выполнить последнее действие, которым является сложение. Для начала приведём эти числа к общему знаменателю, сложим и выделим целую часть:
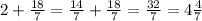
Вот и ответ.