Пошаговое объяснение:
z = x²y - 2xy - 3x² - y² + 6x - 9y
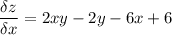
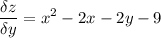
теперь решаем систему
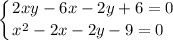
из второго уравнения выражаем у и подставляем в первое уравнение
у = х²/2 - х - 9/2
2x(х²/2 - х - 9/2) -6x -2(х²/2 - х - 9/2) +6 =0
x³ -3x² -13x +15 =0 ⇒x₁= -3; y₁=3; x₂=1; y₂= -5; x₃=5; y₃=3
мы получили три критические точки
M₁(1;-5), M₂(-3;3), M₃(5;3)
но пока не знаем, кто из них минимум, кто максимум
поэтому ищем частные производные второго порядка
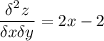
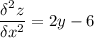
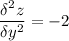
теперь будем считать значение вторых производных в кажной точке
M₁(1;-5)
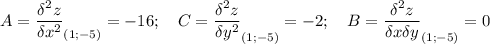
AC - B² = 32 > 0 и A < 0 , то в точке M₁(1;-5) максимум z(1;-5) = 28
M₂(-3;3)
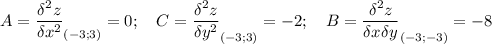
AC - B² = -64 < 0, то в точке M₂(-3;3) глобального экстремума нет.
M₃(5;3)
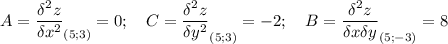
AC - B² = -64 < 0, то точке M₂(5;3) глобального экстремума нет.
ответ
функция имеет один экстремум
в точке M₁(1;-5) и это максимум z(1;-5) = 28;
1) к обеим частям неравенства 8 < 13 прибавить число: 5; 4
8+5 < 13+5 ⇔ 13 < 18
8+4 < 13+4 ⇔ 12 < 17
2) обе части неравенства 18 > 6 умножить на: 4; 5; -1, -0,5; 11
18 > 6 | ·4 ⇔ 18 · 4 > 6 · 4 ⇔ 72 > 24
18 > 6 | ·5 ⇔ 18 · 5 > 6 · 5 ⇔ 90 > 30
18 > 6 | ·(-1) ⇔ 18 · (-1) < 6 · (-1) ⇔ -18 < -6
18 > 6 | ·0) ⇔ 18 · 0=6×0⇔0=0
3) обе части неравенства 24 > 12 умножить на: 2; 3; 4
24 > 12 | ·2 ⇔ 24 · 2 > 12 · 2 ⇔ 48 > 24
24 > 12 | ·3 ⇔ 24 · 3 > 12 · 3 ⇔ 72 > 36
24 > 12 | ·4 ⇔ 24 · 4 > 12 · 4 ⇔ 96 > 48
2) 1\2 + 6 3\7 = 7\14 + 6 6\14 = 6 13\14
3) 6 + 4 9\11 = 10 9\11
4) 3 3\4 + 7\9 = 3 27\36 + 28\36 = 3 55\36 = 4 19\36
5) 2\9 + 1 8\15 = 10\45 + 1 24\45 = 1 34\45
6) 1\14 + 9 3\7 = 1\14 + 9 6\14 = 9 7\14 = 9 1\2 = 9.5
7) 9 + 4 5\16 = 13 5\16
8) 7 1\2 + 6 = 13 1\2 = 13.5
9) 5\7 + 3 1\4 = 20\28 + 3 7\28 = 3 27\28