1) 1,7*4,92*7,2 47,664
= = 2,37
4,8*0,82*5,1 20,0736
2) 2 1/3*1 1/7*1 1/5 7/3 х 8/7 х 6/5 336/105
= = = 336/105 : 11844/ 105 =
3 3/5*4 2/3*6 5/7 18/5 х 14/3 х 47/7 11844/105
336 х 105 336
= сокращаем на 105 = = 0,03
105 х 11844 11844
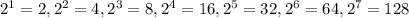и т.д.
Получаем, что двойка в степенях оканчивается на 2, 4, 8, 6, далее снова на 2, 4, 8, 6 и так до бесконечности. Используем закономерность "четвёрок" этих чисел.
32 делится на 4, значит 2 в степени 32 заканчивается цифрой 6
69 не делится на 4, зато 68 делится на 4, получаем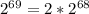 
Произведение двойки и числа, оканчивающегося на 6 равно 12, т.е. оно оканчивается на 2
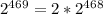468 делится на 4, значит аналогично предыдущему произведение
заканчивается цифрой 2
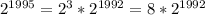
Произведение 8 и 6 равно 48, значит всё произведение заканчивается на 8
Так и объясняйте ребёнку! Успеха!
y=4^(x^2-2x+5)
Решение
Показательная функция вида у= a^x с основанием а = 4 > 1(возрастающая функция) принимает наименьшее значение при минимальном значении аргумента. Поэтому необходимо найти минимальное значение квадратного трехчлена x^2-2x+5.
На графике y = x^2-2x+5 - это парабола с ветвями вверх( так как коэффициент при х^2 больше нуля 1>0) и минимумом (вершиной) параболы находящейся в точке
x = -(-2)/(2*1) =1 ( вершина параболы вида ax^2+dx+с находится по формуле х=-b/(2a))
Поэтому минимальное значение функции равно
y=4^(1^2-21+5) = 4^4 =256
ответ: ymin = 256
Можно также провести исследование этой функции
y=4^(x^2-2x+5)
Производная
y' = (4^(x^2-2x+5))' = 4^(x^2-2x+5)*(ln(4))*(x^2-2x+5)'= 4^(x^2-2x+5)*(ln(4))*(2x-2)
Определим критические точки
y' = 0 или 4^(x^2-2x+5)*(ln(4))*(2x-2) =0
2х - 2 = 0
х = 1
Определим методом подстановки знаки первой производной и нанесем их на числовую ось
- 0 +
!
1
Таким образом видно, что в точке х=1 функция имеет минимум.
y=4^(1^2-21+5) = 4^4 =256