ответ и Пошаговое объяснение:
Дано уравнение
3·x²–x·y+x–2·y=3.
Преобразуем уравнение:
3·x²+x–3=x·y+2·y
y·(x+2)=3·x²+x–3
Так как х = –2 не является корнем уравнения:
3·(–2)²–(–2)·y+(–2)–2·y=12+2·y–2–2·y=12–2=10≠3,
то делим на (х+2):
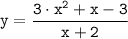
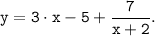
По условию нужно решить уравнение в целых числах. Последнее выражение показывает, что если x+2 является делителем 7, то неизвестная y принимает целые значения.
Значит, выражение x+2 может принимать значения: ±1, ±7. Отсюда:
x+2 = –1 ⇒ х = –3 ⇒ у = 3·(–3)–5–7 = –21 ⇒ (х; у) = (–1; –21);
x+2 = 1 ⇒ х = –1 ⇒ у = 3·(–1)–5+7 = –1 ⇒ (х; у) = (1; –1);
x+2 = –7 ⇒ х = –9 ⇒ у = 3·(–9)–5–1 = –33 ⇒ (х; у) = (–7; –33);
x+2 = 7 ⇒ х = 5 ⇒ у = 3·5–5+1 = 11 ⇒ (х; у) = (7; 11).
х=6.
Пошаговое объяснение:
Выполним деление смешанных чисел, для этого представим смешанные числа в виде неправильной дроби и выполним деление .
Чтобы записать смешанное число в виде неправильной дроби можно:
1)знаменатель умножить на целую часть;
2) к произведению прибавить числитель дробной части;
3) полученную сумму записать в числитель, а знаменатель оставить без изменений.
Чтобы разделить одну дробь на другую, надо делимое умножить на дробь, обратную делителю.

Тогда неравенство принимает вид
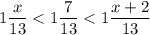
Найдем натуральные значения х, удовлетворяющие неравенству
при х= 6
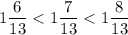
0,5632:5,12+42,56:3,8-(11-3,9-:1,5)= 2,91
1) 3,9:1,5=2,6
2) 11-2,6=8,4
3) 0,5632:5,12=0,11
4) 42,56:3,8= 11,2
5) 0,11+11,2=11,31
6) 11,31-8,4= 2,91