Итак получили 2 решения, теперь обратим внимание на условие: , что под ним подразумевалось изначально, я не уверен, может быть этим условием хотели сказать что нас интересуют только действительные корни уравнения и мы не рассматриваем пространство комплексных корней, но скорее всего здесь это было сделано для того чтобы ограничить область в которой лежат нули первообразной, областью следующего вида: . Будем полагать что это так, тогда нули первообразной лежат на данном отрезке при n=1, и первый корень вообще не будет лежать на отрезке при любых значениях k
Линк-вымышленный персонаж и основной проьагонист в серии видеоигр the legend of Zelda А Бен Утопленник-парень, который любил игры про the legend of Zelda. Когда он умер, Бен стал играть Линка(я так думаю) Вот цитата из истории "История описывает, как умер Бен Утопленник, именно таким образом. Парень ушел в другой мир несчастливым, злым, проклинающим и мечтающим о любимой игре. Можно было поставить здесь точку, но ему удалось осуществить задуманное и отомстить за свою смерть. Когда тело парня было найдено, его мама решила отдать соседу все игры, так как искренне верила, что для Бена он был другом. Придя домой, Джек включил игру «Majora’s Mask» и там он увидел статую Линка, которая не покидала экран. Он увидел странную картину: Линк погружался в воду и тонул, а после появилась страшная надпись: «Ты не должен был этого делать!». На следующий день Джека нашли повешенным, а на экране находилась улыбающаяся статуя Линка." Так что я думаю что разница не большая
Приведем данную гиперболу к каноническому виду: 2x^2-9y^2=18 x^2/9-y^2/2=1 x^2/3^2-y^2/(sqrt(2))^2=1 (примечание: sqrt - квадратный корень) Найдем вершины гиперболы: y=0 x^2/9=1 x^2=9 x1=3 x2=-3 точки (-3;0) и (3;0) - вершины гиперболы Найдем уравнение окружности, проходящей через точки (-3;0), (3;0) с центром в точке А(0;4): уравнение окружности с центром в точке (0;0) имеет вид x^2+y^2=R^2 (R - радиус окружности) центр заданной окружности смещен вдоль оси y вверх на 4, т.к. точка А имеет координаты (0;4): x^2+(y+4)^2=R^2 По теореме Пифагора найдем радиус окружности: R=sqrt((3-0)^2+(4-0)^2)=sqrt(9+16)=sqrt(25)=5
Найдем интеграл от f(x)
Получаем:
Надо найти C.
Известно что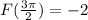
Подставим в найденное F(x), получим:
Получили, что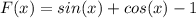
Дальше надо решить уравнение:
Итак получили 2 решения, теперь обратим внимание на условие:![f: [\pi;2\pi] \to R](/tpl/images/0070/1780/e655c.png) , что под ним подразумевалось изначально, я не уверен, может быть этим условием хотели сказать что нас интересуют только действительные корни уравнения и мы не рассматриваем пространство комплексных корней, но скорее всего здесь это было сделано для того чтобы ограничить область в которой лежат нули первообразной, областью следующего вида:
, что под ним подразумевалось изначально, я не уверен, может быть этим условием хотели сказать что нас интересуют только действительные корни уравнения и мы не рассматриваем пространство комплексных корней, но скорее всего здесь это было сделано для того чтобы ограничить область в которой лежат нули первообразной, областью следующего вида: ![x \in [\pi; 2\pi]](/tpl/images/0070/1780/72d02.png) . Будем полагать что это так, тогда нули первообразной
. Будем полагать что это так, тогда нули первообразной 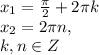 лежат на данном отрезке при n=1, и первый корень вообще не будет лежать на отрезке при любых значениях k
лежат на данном отрезке при n=1, и первый корень вообще не будет лежать на отрезке при любых значениях k
таким образом получается, что:
Подводя итог получаем
Нулями производной будут: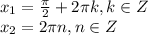
Однако условию![f: [\pi;2\pi] \to R](/tpl/images/0070/1780/e655c.png) удовлетворяет только
удовлетворяет только 
ответ: