ответ: ряд сходится, при решении задачи использован признак сравнения.
Пошаговое объяснение:
Сравним это ряд с рядом обратных квадратов ∑1/n², который, как известно, сходится. Для этого составим разность 1/n²-(n+1)/(n⁴+1)=(n⁴-n³-n²+1)/[n²*(n⁴+1)]. Так как знаменатель этой дроби положителен при любом n, то её знак будет зависеть от знака числителя n⁴-n³-n²+1. Но n⁴-n³-n²+1=n²*[(n-1/2)²-5/4]+1=n²*(n-1/2)²-5/4*n²+1. Отсюда следует, что числитель обращается в ноль лишь при n=1; если же n>1, то он положителен, а это значит, что при n>1 1/n²>(n+1)/(n⁴+1). Поэтому данный ряд сходится.
Площадь квадрата равна квадраты его стороны, пусть сторона квадрата равна a, тогда a^2 = 36 см^2
a = 6 см.
Площадь серого многоугольника состоит из одного квадрата, четырёх прямоугольник и четырёх треугольников.
Площадь квадрата равна 36 см^2
Площадь одного прямоугольника равна 6 * (6/2) = 6 * 3 = 18 см^2. Так как одно сторона совпадает со стороной квадрата, а другая с половиной стороны квадрата. Значит площадь четырёх прямоугольников: 4 * 18 = 72 см^2.
Треугольнике прямоугольные, также они равнобедренные, катеты их равны половине стороны квадрата, то есть 6 : 2 = 3 см. Значит площадь одного треугольника:
(3 * 3) / 2 = 4.5 см^2
Откуда площадь четырёх треугольников:
4.5 * 4 = 18 см^2
Сложим все площади:
36 + 72 + 18 = 126 см^2
ответ: S = 126 см^2
3584
Пошаговое объяснение:
Пусть в сборнике n задач, тогда:
За 1 день решено: n/2+1
За 2 день решено: n/4+2
За 3 день решено: n/8+3
...
За 7 день решено: n/2^7+7
Сложим решенные за все дни задачи, причём дроби вида n/2^k (k - от 1 до 7) отделим от вторых слагаемых каждого дня:
(n/2+n/4+...+n/256)+(1+2+...+7)=n
Вынесем n из первой скобки:
n*(1/2+1/4+...+1/256)+(1+2+...+7)=n
Первая скобка (без n) - сумма первых семи членов геометрической прогрессии со знаменателем 1/2.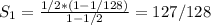
Вторая скобка - сумма первых семи членов арифметической прогрессии с разностью 1