Числа больше нуля считаются положительными (пример: 1 2 3 4 5 6 ...)
Числа меньше нуля считаются отрицательными (пример: -1 -2 -3 -4 -5 -6 ...)
Рассмотрим примеры:
6-4=2 (ну думаю что это очевидно)
8*2-(7-3+4) = (обрати внимание что перед скобкой стоит минус, значит после раскрытия скобки, знаки внутри скобки меняются, т.е. минус в плюс, а плюс в минус), тогда решение будет таким:
16-7+3-4=8
Допустим дано уравнение:
8-y=0
Цифру переносим в правую сторону, а y остаётся (вспоминаем, что при переносе знак меняется в противоположную)
-y=-8
Если обе стороны минусы, то они автоматически становятся плюсовыми
y=8
Также если допустим в ответе
-y=8
то минус переносится в правую сторону, следовательно:
y=-8.
Если умножить две минусовые цифры друг на друга, то они станут плюсовыми, пример:
-4*(-4)=4*4=16.
Также если вычесть с маленького числа большую, то он уйдёт в минус, пример:
4 - 7 = -3
Думаю что все основы рассказал что да как
Задача на подобие треугольников (коэффициенты подобия).
В первом треугольнике - стороны 4 см, 6 см и 9 см.
Во втором треугольнике - стороны X см, Y см и 36 см.
*в первом треугольнике самая большая сторона - 9 см, во втором треугольнике - 36 см (бóльшая сторона одного треугольника соотносится с большей стороной второго треугольника).
Значит они относятся с каким-то коэффициентом подобия (раз по условию треугольники подобны):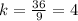 
(бóльшая сторона большего треугольника разделить на бóльшую сторону меньшего треугольника).
Соответственно, теперь по этому коэффициенту можно найти оставшиеся стороны:
Первая сторона -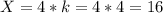 
см
Вторая сторона -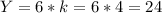 
см
Третья сторона -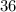 
см (по условию)
Периметр большего треугольника: 
см.
*дополнительно это можно и проверить. Периметры подобных треугольников соотносятся как коэффициент подобия:
Периметр меньшего треугольника: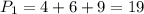 
см
Тогда поделив периметр большего треугольника на меньшего треугольника мы будем должны получить этот самый коэффициент подобия (то есть 4):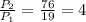 
- значит задача решена верно!
ответ: 76 см.
h = √51 + √149 ≈ 19,3 м
h = √149 - √51 ≈ 5 м
Пошаговое объяснение:
Высота равнобедренного треугольника, проведенная к основанию, является медианой.
Обозначим высоту h, половину основания а.
Площадь треугольника равна половине произведения основания на высоту:
S = ah,
по теореме Пифагора составим второе уравнение:
a² + h² = 400
Получаем систему уравнений:
ah = 98 (1)
a² + h² = 400
Домножим первое уравнение на 2 и вычтем из второго:
2ah = 196
a² - 2ah + h² = 204 (2)
2) (a - h)² = 204
|a - h| = √204
|a - h| = 2√51
Возможны два случая:
1. a < h
h - a = 2√51
a = h - 2√51
Подставим выражение в (1):
h² - 2√51h - 98 = 0
D/4 = 51 + 98 = 149
h = √51 - √149 - не подходит по смыслу задачи
h = √51 + √149 ≈ 19,3 м
2. a > h
a - h = 2√51
a = h + 2√51
Подставим в (1):
h² + 2√51h - 98 = 0
D/4 = 51 + 98 = 149
h = - √51 - √149 - не подходит по смыслу задачи
h = - √51 + √149 = √149 - √51 ≈ 5 м
____________________________________________
Применена формула сокращенного дискриминанта при решении квадратного уравнения:
ax² + bx + c = 0
D/4 = (b/2)² - ac
x = (- b/2 ± √(D/4)) / a