Дано: S = 330 км; v₁ = 75 км/ч; v₂ = 100 км/ч; t₀ = 1 ч
Найти: t - ?; S₂ - ?
Скорость сближения мотоцикла и автобуса:
v = v₂ - v₁ = 100 - 75 = 25 (км/ч)
Расстояние между мотоциклом и автобусом в момент старта мотоцикла:
S₀ = v₁t₀ = 75 * 1 = 75 (км)
Время, за которое мотоциклист догонит автобус:
t = S₀/v = 75 : 25 = 3 (ч)
До момента встречи мотоциклист проедет:
S₁ = v₁t = 100*3 = 300 (км)
Расстояние, оставшееся до города Б:
S₂ = S - S₁ = 330 - 300 = 30 (км)
ответ: Саша догонит автобус за 3 часа. Оставшееся расстояние до города Б - 30 км
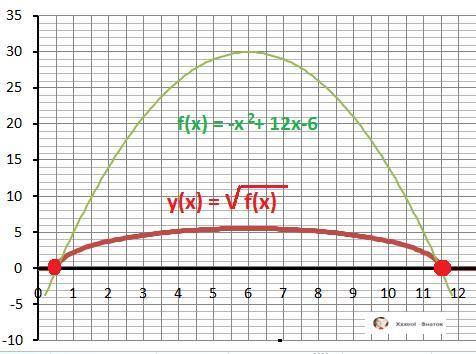
Дано: y(x) = √(-x²+12*x-6)
Найти: Значения Х при минимальных значениях y(x).
1. Функция y(x) = √f(x) - существует при f(x) ≥ 0.
2. Находим точки f(x)=0 - под знаком радикала.
Решение.
1) f(x) = - x² + 12*x - 6 - функция под знаком корня.
2) Решаем квадратное уравнение f(x) = 0, находим дискриминант и корни уравнения.
D = 12² - 4*(-1)*(-6) = 144-24 = 120 - дискриминант.
√D = √120 = √(2²*30) = 2√30.
x₁ = 6 - √30, x₂ = 6 + √30 - корни квадратного уравнения. Получили область определения функции y(x):
X∈[x₁;x₂] - ООФ y(x). Минимальные значения функция на границах отрезка.
Ymin(x)=0 при x₁ = 6 - √30, x₂ = 6 + √30 - ответ.
Дополнительно - графики функций - в приложении.
Максимальное значение функции y(x) равно:
Ymax(6) = √30 (≈ 5,48).
4=1/4
4:1/4=4*4/1=16 (см) - длина
16-4=12 (см) - ширина
(12+16)*2=56 (см) - периметр
12*16=192 (см) - площадь