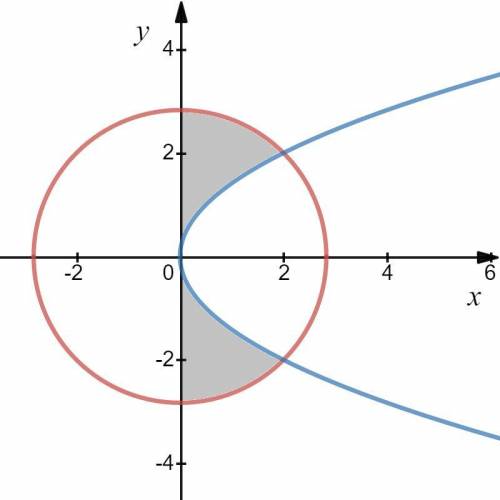
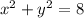— уравнение окружности с центром 
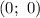и радиусом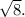 
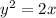— уравнение параболы
Изобразим графики данных уравнений и найдем площадь образовавшейся фигуры в правой полуплоскости.
Выразим ординаты данных уравнений:
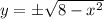и 
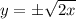
Так как имеем симметричные фигуры, найдем площадь 
одной из них. Общая их площадь 
будет состоять из площади двух 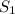, то есть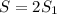 
Тогда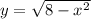 
и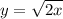 
. Поэтому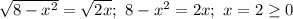 
Так как окружность вытесняет больше площади, чем парабола, то имеем разность их площадей, определяющаяся через определенный интеграл:
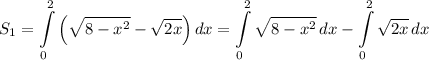
Найдем первый интеграл геометрически: площадь круга находится по формул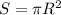е 
, где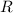 
— радиус круга. Тогда четверть круга: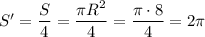 
Найдем второй интеграл по формуле Ньютона-Лейбница:
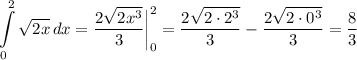
Таким образом,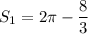 
кв. ед.
Тогда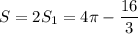 
кв. ед.
ответ: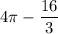 
кв. ед.
Пусть 
грн стоит один килограмм апельсинов, а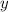 
грн — один килограмм лимонов. Тогда 5 кг апельсинов будут стоить 
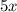грн, а 4 кг лимонов — 
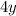грн, что вместе составляет 22 грн, то есть 
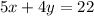. Также 6 кг апельсинов будут стоить 
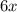грн, а 2 кг лимонов — 
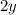грн, что вместе составляет 18 грн, то есть 
.
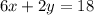Имеем систему из двух линейных уравнений:
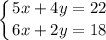
Домножим второе уравнение на 2:
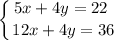
Вычтем из второго уравнения первое:
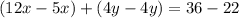
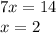
Тогда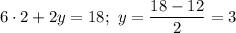 
Таким образом, 2 грн стоит один килограмм апельсинов и 3 грн стоит один килограмм лимонов.
ответ: 2 грн и 3 грн.
Это свойство пропорций:
1)х/15=0,25/3
х=15*0,25:3
х=2,5
2)7/y+2=2/0,6
7/у=2/0,6-2
7/у=10/3-2
7/у=4/3
у=7:4/3
у=5,25
3)266/2+15z=14/23
133+15z=14/23
15z=14/23-133
15z=-3045/23
z=-3045/23:15
z=-203/23=-8 19/23
4)3/2t-5=5/4
3t/2-5=5/4
3t*2-5*4=5
6t-20=5
6t=5+20
6t=25
t=25:6
t=4 1/6