(Метод Лагранжа).
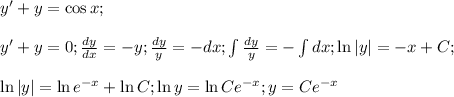
Произвольную постоянную примем за функцию от 
.
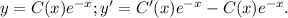
Подставим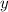 
и 
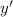в исходное уравнение:
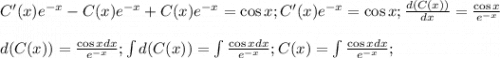
Отдельно найдем полученный неопределенный интеграл:
![\int\frac{\cos{x}dx}{e^{-x}}=\int{e^x\cos{x}}dx;int{e^x\cos{x}}dx=\left[u=e^x; du=e^xdx\atop dv=\cos{x}dx;v=\sin{x}\right]=e^x\sin{x}-\int{e^x\sin{x}dx.}int{e^x\sin{x}dx=\left[u=e^x; du=e^xdx\atop dv=\sin{x}dx;v=-\cos{x}\right]=-e^x\cos{x}+\int{e^x\cos{x}}dx.](/tpl/images/4806/5534/da0d3.png)
Отсюда получаем что:
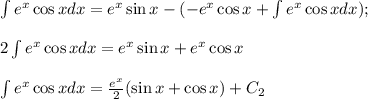
Отсюда получаем что:
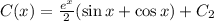
Теперь подставим в формулу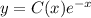 
:
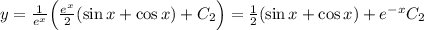
В итоге окончательно получаем:
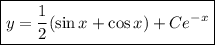
(Метод Бернулли)
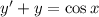
Пусть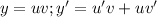 
тогда:
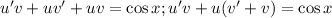потребуем, чтобы 
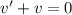тогда:
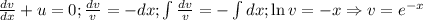
Подставим найденное значение 
в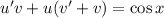 
:
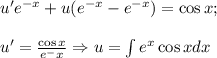
В предыдущем данный интеграл был найден методом интегрирования по частям, поэтому не будет здесь его искать а просто подставим уже найденный.
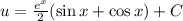но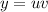 
тогда:
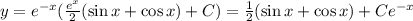Отсюда получаем:
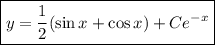
Составим множество А. Выпишем нечётные натуральные числа из отрезка от 3 до 9:
3; 5; 7; 9
Теперь возведем их в квадрат:
9; 25; 49; 81
Значит:
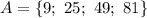
Составим множество В. Выпишем целые числа из интервала от 3 до 10:
4; 5; 6; 7; 8; 9
Умножим их на 7:
28; 35; 42; 49; 56; 63
Значит:
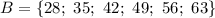
Находим пересечение множеств А и В. В пересечение попадают элементы, принадлежащие одновременно и множеству А и множеству В:
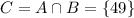
Находим объединение множеств А и В. В объединение попадают элементы, принадлежащие хотя бы одному из множеств А или В:
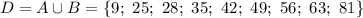
вот 2 задание:
6; 2√10; 3√5.