1.
Выберите правильный ответ. Какие из высказываний (высказывательных форм) в следующих парах являются отрицаниями друг друга:
5<10 и 5>10
10>9 и 10<=9
Существуют белые слоны. Все слоны серые.
Этот треугольник равнобедренный и прямоугольный.
Этот треугольник не равнобедренный или он не прямоугольный.
Прямая а параллельна прямой b.
Прямая a перпендикулярна прямой b.
2.
Выберите правильный ответ. Ложными высказываниями являются . . .
Наличия аттестата о среднем образовании достаточно для поступления в институт
Наличие аттестата о среднем образовании необходимо для поступления в институт
Если целое число делится на 6, то оно делится на 3
Для того, чтобы четырёхугольник был квадратом, необходимо, чтобы его диагонали были равны и перпендикулярны
3.
Выберите правильный ответ. Истинными высказываниями являются . . .
Для того, чтобы четырёхугольник был квадратом, достаточно, чтобы его диагонали были равны и перпендикулярны
Наличие аттестата о среднем образовании необходимо для поступления в институт
Если целое число делится на 6, то оно делится на 3
Каждый ромб является параллелограммом
Каждый параллелограмм является ромбом
4.
Выберите правильный ответ. Объединение двух высказываний в одно с союза «и» называется…
инверсия
конъюнкция
дизъюнкция
импликация
5.
Выберите правильный ответ. Логической операцией не является…
логическое умножение
логическое деление
логическое отрицание
логическое сложение
6.
Выберите правильный ответ. Укажите логическую операцию, которая не является базовой:
конъюнкция
инверсия
эквивалентность
дизъюнкция
7.
Выберите правильный ответ. Используя логические высказывания А ="Это утро ясное", В= "Это утро теплое", выразите формулу А=>не В на обычном языке:
Это утро ясное или не тёплое
Если это утро ясное, то оно не тёплое
Если утро теплое, то оно и ясное
Это утро не ясное, но теплое
Покажем, что последняя цифра не может быть двойкой. Действительно, если это так, то пусть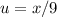 
. Тогда 
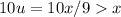, но поскольку эти числа отличаются лишь последней цифрой (и 2>0), то 
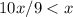, противоречие.
Это был один из начать рассуждение, которое, однако, вряд ли к чему либо приведет.
Рассмотрим другой подход. Заметим, что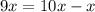 
. Пусть исходное число построено так: 
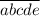. Пусть 
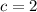. Тогда ![\overline{abced}=9\times \overline{abed}=\overline{abed0}-\overline{abed}\leq \overline{a[b-1]ed0}](/tpl/images/1428/2431/04d5d.png)
, противоречие. Аналогично доказывается для любой позиции двойки в числе, кроме второй слева. Идея состоит в том, что вычитаемое четырехзначное число достает таким образом до позиции, которая остается в числе, а значит, нарушает равенство. Остается лишь сделать так, чтобы эта позиция исчезала. Собственно, поставить двойку на вторую позицию
Теперь рассмотрим вычитание столбиком:
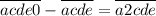, откуда ясно, что 
, 
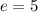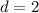или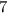 
, но два быть не может, поскольку у нас ровно одна двойка, 
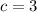или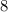 
, наконец 
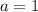или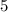 
.
Получаем два числа: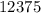 
и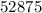 
.
1 час - 11 ц 14/25 - 6ц 7/25 = 5 ц 7/25
2 час - 11 ц 14/25 - 2 ц 8/25 - 5ц 7/25 = 3ц 24/25