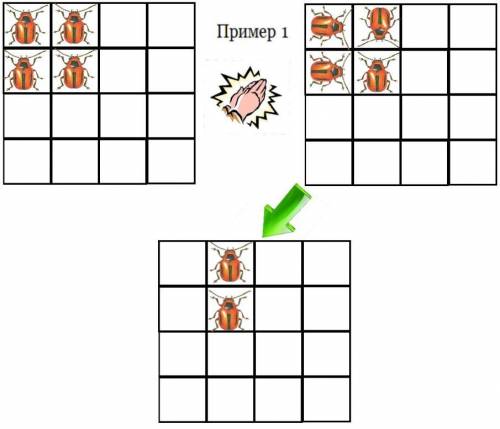
Рассмотрим несколько случаев. Если мы будем стараться переместить жуков в центр, то нам обязательно придётся занять и 1 боковую клетку (пример 1). Не будем полностью заполнять доску жуками. Рассмотрим лишь часть. Выходит, что задействуя 4 клетки, мы можем получить 2 свободных.
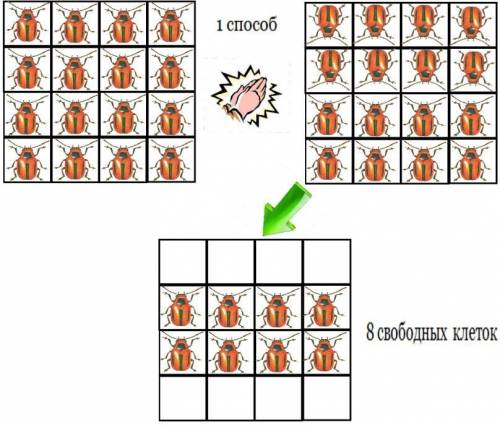
Попробуем схожим методом получить максимальное кол-во свободных клеток. См У нас вышло 8 свободных клеток.
Попытаемся сделать лучше.
Заметим, что если мы будем намерены занять одну из клеток, то обязательно какая-то соседняя клетка с данной будет обладать жуком (тоже занята).
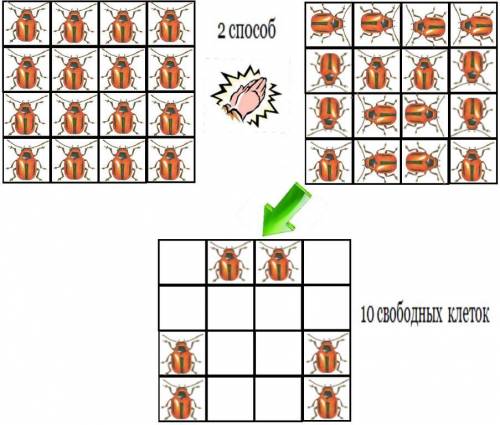
Попробуем расставить эти будущие занятые клетки по бокам доски (т.к. в центре уже пробовали). См Улучшить данный результат у нас никак не выйдет. Если мы попытаемся как-то освободить одну из клеток, то тогда одному из жуков будет просто некуда бежать.
ответ: максимальное количество пустых клеток - 10.
В решении.
Пошаговое объяснение:
3. Реши данное неравенство.
|2x + 1| + 2 > 3
|2x + 1| > 3 - 2
|2x + 1| > 1
Схема:
2x + 1 > 1 2x + 1 < -1
2x > 1 - 1 2x < -1 - 1
2x > 0 2x < -2
x > 0 x < -1
Решение неравенства: х∈(-∞; -1)∪(0; +∞), объединение.
Неравенство строгое, скобки круглые.
4. Решите неравенства и запишите множество их целых решений:
(|x + 2| + 3)/2 <= 5
Умножить все части неравенства на 2, чтобы избавиться от дробного выражения:
|x + 2| + 3 <= 10
|x + 2| <= 10 - 3
|x + 2| <= 7
Схема:
x + 2 <= 7 x + 2 >= -7
х <= 7 - 2 x >= -7 - 2
x <= 5 x >= -9
Решение неравенства: х∈[-9; 5], пересечение.
Неравенство нестрогое, скобки квадратные.
Целые решения неравенства:
-9; -8; -7; -6; -5; -4; -3; -2; -1; 0; 1; 2; 3; 4; 5.
Z { -9; -8; -7; -6; -5; -4; -3; -2; -1; 0; 1; 2; 3; 4; 5}. Скобки фигурные.
Обозначение на числовой прямой:
начертить прямую, отметить значения -9,-8,...0, 1, 5 и нанести штриховку от -9 до 5. У значений х= -9 и х= 5 кружочки закрашенные.
ответ: 1 место - Оля 2 место - Маша 3 место - Настя .. 4 место - Лена