Обозначим: собственная скорость теплохода — v км/ч, а скорость течения реки — x км/ч». Тогда
a) v + x (км/ч) - скорость теплохода по течению реки
v - x (км/ч) - скорость теплохода против течения
b) 3*(v+x) (км) - расстояние, которое теплоход проплыл за 3 часа по течению реки
c) 3,9*(v-x) (км) - расстояние, которое теплоход проплыл за 3,9 ч против течения реки
d) расстояние, пройденное теплоходом по течению реки, и расстояние, пройденное теплоходом против течения реки, будут равными, т. е.
3*(v+x)=3,9*(v-x)
Пошаговое объяснение:
Пройденное расстояние равно скорости, умноженной на время:
s = v × t.
В нашем случае расстояние не меняется. Разными являются скорость теплохода (при движении по течению реки она больше) и затраченное время (при движении по течению реки оно меньше).
V=64π кубических единиц объем искомого конуса.
Пошаговое объяснение:
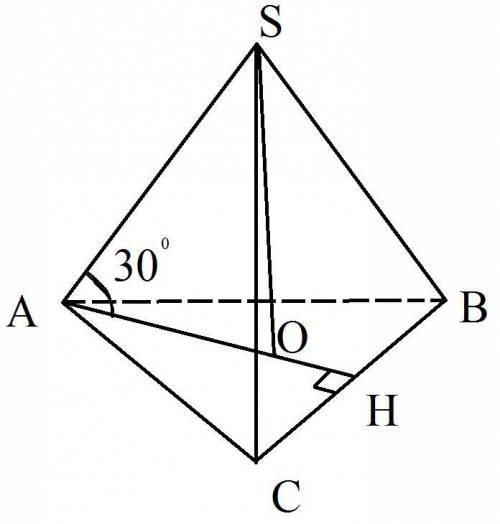
Рисунок смотрите в приложении.
Объем конуса вычисляется по формуле
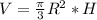 (*).
(*).
Здесь R - радиус основания конуса, Н - высота конуса.
Найдем радиус основания конуса. Он равен радиусу описанной окружности основания пирамиды.
SO - высота конуса. Точка О - центр вписанной и описанной окружности правильного треугольника.
АО=R - длина радиуса описанной окружности.
Радиус описанной окружности вычисляется по формуле
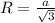 , где а - это длина стороны треугольника.
, где а - это длина стороны треугольника.
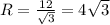 единиц.
единиц.
Из ΔАОS, который по построению прямоугольный (∠О=90°), по условию задачи ∠SAO=30°. Так как это и есть угол между ребром и основанием пирамиды. Теперь из этого треугольника можно найти SO. SO=AO*tg∠SAO. SO=AO*tg30°,
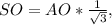
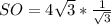 ,
,
SO=4 единицы.
Подставим в формулу (*).
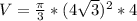 ,
,
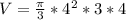
V=π*4³ кубических единиц.
V=64π кубических единиц.
2) 290 / 100 * 104,5 = 303,05
3) 33 / 100 * 57 = 18,81
4) 220 / 100 * 55 = 121
5) 4502 / 100 * 165 = 7428,3
6) 0,3 / 100 * 348 = 1,044
7) 0,012 / 100 * 67 =0,00804
8) 0,1 / 100 * 900 = 0,9
9) 2,52/100 * 12000 = 302,4
10) 39/100 * 0,045 = 0,01755